题目内容
三棱锥S-ABC的所有顶点都在球O的表面上，SA⊥平面ABC，AB⊥BC，又SA=AB=BC=2，则球O的表面积为 ．
考点：球的体积和表面积
专题：计算题,空间位置关系与距离
分析：根据题意，三棱锥S-ABC扩展为正方体，正方体的外接球的球心就是正方体体对角线的中点，求出正方体的对角线的长度，即可求解球的半径，从而可求三棱锥S-ABC的外接球的表面积．
解答：
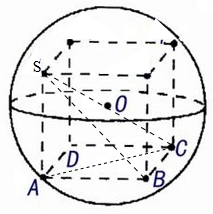解：三棱锥S-ABC的所有顶点都在球O的表面上，SA⊥平面ABC，AB⊥BC，又SA=AB=BC=2，
三棱锥扩展为正方体的外接球，外接球的直径就是正方体的对角线的长度，
∴球的半径R=
=
．
球的表面积为：4πR2=4π•（
）2=12π．
故答案为：12π．
解：三棱锥S-ABC的所有顶点都在球O的表面上，SA⊥平面ABC，AB⊥BC，又SA=AB=BC=2，三棱锥扩展为正方体的外接球，外接球的直径就是正方体的对角线的长度，
∴球的半径R=
| 1 |
| 2 |
| 4+4+4 |
| 3 |
球的表面积为：4πR2=4π•（
| 3 |
故答案为：12π．
点评：本题考查三棱锥S-ABC的外接球的表面积，解题的关键是确定三棱锥S-ABC的外接球的球心与半径．
练习册系列答案
期末100分闯关海淀考王系列答案
相关题目
己知a∈R，则“a=±1”是“a2-1+（a-1）i为纯虚数”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
如图，电键A、B、C、D闭合的概率分别为p1、p2、p3、p4，且彼此独立，求灯泡亮的概率．已知tanα=2，tanβ=3，且α、β都是锐角，则α+β=（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|