题目内容
解下列不等式
（1）
x2-4x+6＜0；
（2）
≥3．
（1）
| 1 |
| 2 |
（2）
| 4x2-20x+18 |
| x2-5x+4 |
考点：一元二次不等式的解法
专题：不等式的解法及应用
分析：（1）利用一元二次不等式的解法即可得出；
（2）把分式不等式等价转化为整式不等式，利用“穿根法”即可得出．
（2）把分式不等式等价转化为整式不等式，利用“穿根法”即可得出．
解答：
解：（1）原不等式化为x2-8x+12＜0，因式分解为（x-2）（x-6）＜0，解得2＜x＜6．
∴原不等式的解集为{x|2＜x＜6}．
（2）原不等式可化为
-3≥0
?
≥0
?
≥0，
?（x-1）（x-2）（x-3）（x-4）≥0，且x≠1，4．
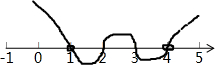
利用“穿根法”，如图所示，
∴x∈（-∞，1）∪[2，3]∪（4，+∞）．
解：（1）原不等式化为x2-8x+12＜0，因式分解为（x-2）（x-6）＜0，解得2＜x＜6．∴原不等式的解集为{x|2＜x＜6}．
（2）原不等式可化为
| 4x2-20x+18 |
| x2-5x+4 |
?
| x2-5x+6 |
| x2-5x+4 |
?
| (x-2)(x-3) |
| (x-1)(x-4) |
?（x-1）（x-2）（x-3）（x-4）≥0，且x≠1，4．
利用“穿根法”，如图所示，
∴x∈（-∞，1）∪[2，3]∪（4，+∞）．
点评：本题考查了一元二次不等式的解法、把分式不等式等价转化为整式不等式、“穿根法”，考查了计算能力，属于基础题．
练习册系列答案
相关题目
将函数y=cos（
x-
）的图象上各点向左平移
个单位，所得函数图象的一条对称轴是（ ）
| 1 |
| 2 |
| π |
| 3 |
| π |
| 6 |
A、x=
| ||
B、x=
| ||
| C、x=π | ||
D、x=
|
某工厂某种产品的产量y（千件）与单位成本x（元）之间的关系满足y=60-2.5x，则以下说法正确的是（ ）
| A、产品每增加1 000 件，单位成本下降2.5万元 |
| B、产品每减少1 000 件，单位成本上升2.5万元 |
| C、产品每增加1 000 件，单位成本上升2.5万元 |
| D、产品每减少1 000 件，单位成本下降2.5万元 |
已知a＞b＞c，a+b+c=0，当0＜x＜1时，代数式ax2+bx+c的值是（ ）
| A、正数 | B、负数 |
| C、0 | D、介于-1与0之间 |