题目内容
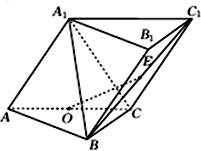 如图,三棱柱ABC-A1 B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,AB=BC且AB⊥BC,O为AC中点.
如图,三棱柱ABC-A1 B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,AB=BC且AB⊥BC,O为AC中点.(1)设E为BC1中点,连接OE,证明:OE∥平面A1AB;
(2)求二面角A-A1B-C1的余弦值.
考点:二面角的平面角及求法,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(1)法一:取BC中点F,连接OF,EF,由已知得面OEF∥面A1AB,由此能证明OE∥平面A1AB.
法二:由已知得OA1⊥平面ABC,以O为原点,OB,OC,OA1所在直线分别为x,y,z轴,建立空间直角坐标系,利用向量法能证明OE∥平面A1AB.
(2)求出平面AA1B的一个法向量和面A1BC1的法向量,利用向量法能求出二面角A-A1B-C1的余弦值.
法二:由已知得OA1⊥平面ABC,以O为原点,OB,OC,OA1所在直线分别为x,y,z轴,建立空间直角坐标系,利用向量法能证明OE∥平面A1AB.
(2)求出平面AA1B的一个法向量和面A1BC1的法向量,利用向量法能求出二面角A-A1B-C1的余弦值.
解答:
(本小题满分12分)
(1)证法一:取BC中点F,连接OF,EF…(1分)
∵E为BC1中点,∴OF∥AB,EF∥BB1,
∴面OEF∥面A1AB.…(3分)
又∵OE?面OEF…(4分)
∴OE∥平面A1AB.…(6分)
证法二:∵AA1=A1C=AC=2,AB=BC且AB⊥BC,O为AC中点,
∴OA1⊥AC.又由题意可知,面AA1C1C⊥底面ABC,
面AA1C1C∩底面ABC=AC,
且OA1?平面AA1C1C,∴OA1⊥平面ABC.
以O为原点,OB,OC,OA1所在直线分别为x,y,z轴,
建立空间直角坐标系.…(1分)
由题意可知,A1A=A1C=AC=2,又AB=BC,AB⊥BC,∴OB=
AC=1,
∴O(0,0,0),A(0,-1,0),A1(0,0,
),C(0,1,0),C1(0,2,
),B(1,0,0),
=(0,1,-
),
=(0,1,
),
=(1,1,0)
设平面AA1B的一个法向量为
=(x,y,z),
则有
,即
,令x=1,得y=-1,z=
,
∴
=(1,-1,
).…(4分)
又∵E是BC1的重点,则E=(
,1,
),∴
=(
,1,
)…(5分)
∵
•
=0,∴OE∥平面A1AB…(6分)
(2)解:平面AA1B的一个法向量
=(1,-1,
),
设面A1BC1的法向量为
=(x,y,z),
则
得
…(8分)
令x=1,所以
=(1,0,
).…(9分)
所以a<
,
>=
=
=
…(11分)
根据图象,得二面角A-A1B-C1的余弦值为-
…(12分)

(1)证法一:取BC中点F,连接OF,EF…(1分)
∵E为BC1中点,∴OF∥AB,EF∥BB1,
∴面OEF∥面A1AB.…(3分)
又∵OE?面OEF…(4分)
∴OE∥平面A1AB.…(6分)
证法二:∵AA1=A1C=AC=2,AB=BC且AB⊥BC,O为AC中点,
∴OA1⊥AC.又由题意可知,面AA1C1C⊥底面ABC,
面AA1C1C∩底面ABC=AC,
且OA1?平面AA1C1C,∴OA1⊥平面ABC.
以O为原点,OB,OC,OA1所在直线分别为x,y,z轴,
建立空间直角坐标系.…(1分)
由题意可知,A1A=A1C=AC=2,又AB=BC,AB⊥BC,∴OB=
| 1 |
| 2 |
∴O(0,0,0),A(0,-1,0),A1(0,0,
| 3 |
| 3 |
| A1C |
| 3 |
| AA1 |
| 3 |
| AB |
设平面AA1B的一个法向量为
| n |
则有
|
|
| ||
| 3 |
∴
| n |
| ||
| 3 |
又∵E是BC1的重点,则E=(
| 1 |
| 2 |
| ||
| 2 |
| OE |
| 1 |
| 2 |
| ||
| 2 |
∵
| n |
| OE |
(2)解:平面AA1B的一个法向量
| n |
| ||
| 3 |
设面A1BC1的法向量为
| m |
则
|
|
|
令x=1,所以
| m |
| ||
| 3 |
所以a<
| m |
| n |
|
| ||||
|
|
|1+
| ||||||||
|
2
| ||
| 7 |
根据图象,得二面角A-A1B-C1的余弦值为-
2
| ||
| 7 |
点评:本题考查直线与平面平行的证明,考查二面角的余弦值的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
已知集合A{x|y=lg(2-x)},集合B={x|-2≤x≤2},则A∩B=( )
| A、{x|x≥-2} |
| B、{x|-2<x<2} |
| C、{x|-2≤x<2} |
| D、{x|x<2} |
已知双曲线C:
-
=1的焦距为10,点P(1,2)在C的渐近线上,则C的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知某空间几何体的三视图如图所示,则( )
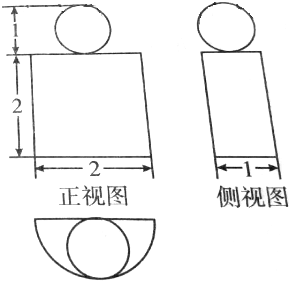

| A、该几何体的表面积为4+2π | ||
B、该几何体的体积为
| ||
| C、该几何体的表面积为4+4π | ||
| D、该几何体的体积为π |
已知实数x,y满足
,若可行域内存在点使得x+2y-a=0成立,则a的最大值为( )
|
| A、-1 | B、1 | C、4 | D、5 |
设a,b,c依次是方程x+sinx=1,x+sinx=2,x+
sinx=2的根,并且0<x<
,则a,b,c的大小关系是( )
| 1 |
| 2 |
| π |
| 2 |
| A、a<b<c |
| B、a<c<b |
| C、c<b<a |
| D、b<c<a |
已知实数x,y满足
,则z=2x-2y-1的取值范围是( )
|
A、[
| ||
| B、[0,5] | ||
C、[
| ||
D、[-
|