题目内容
若a=0.43,b=log30.4,c=30.4,比较a、b、c大小.
考点:对数值大小的比较
专题:函数的性质及应用
分析:利用指数函数与对数函数的单调性即可得出.
解答:
解:∵0<a=0.43<1,b=log30.4<0,c=30.4>1,
∴c>a>b.
∴c>a>b.
点评:本题考查了指数函数与对数函数的单调性,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知f(x)为三次函数,当x=1时f(x)有极大值4,当x=3时,f(x)有极小值0,且函数f(x)过原点,则此函数是( )
| A、f(x)=x3-2x2+3x |
| B、f(x)=x3-6x2+x |
| C、f(x)=x3+6x2+9x |
| D、f(x)=x3-6x2+9x |
设等差数列{an}的前n项和为Sn,若2a8=6+a11,则S9的值等于( )
| A、36 | B、45 | C、54 | D、27 |
不等式ax2-(a+2)x+2≥0(a<0)的解集为( )
A、[
| ||
B、[1,
| ||
C、(-∞,
| ||
D、(-∞,1]∪[
|
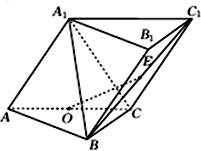 如图,三棱柱ABC-A1 B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,AB=BC且AB⊥BC,O为AC中点.
如图,三棱柱ABC-A1 B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,AB=BC且AB⊥BC,O为AC中点. 如图,P为圆B:(x+2)2+y2=36上一动点,点A坐标为(2,0),线段AP的垂直平分线交直线BP于点Q,求点Q的轨迹方程.
如图,P为圆B:(x+2)2+y2=36上一动点,点A坐标为(2,0),线段AP的垂直平分线交直线BP于点Q,求点Q的轨迹方程.