题目内容
已知角α的终边上一点的坐标为(-1,1),试求三角代数式
•
•
的值.
| tan(540°+x) |
| tan(900°-x) |
| sin(-x) |
| sin(450°-x) |
| cos(360°-x) |
| tan(-x) |
考点:运用诱导公式化简求值
专题:计算题,三角函数的求值
分析:由题意可得x=-1,y=1,r=
,cosα=
=-
,用诱导公式化简后即可求值.
| 2 |
| x |
| r |
| ||
| 2 |
解答:
解:已知角α的终边上一点的坐标为(-1,1),由题意可得x=-1,y=1,
∴r=
,cosα=
=-
.
∴
•
•
=
•
•
=-cosx=
.
∴r=
| 2 |
| x |
| r |
| ||
| 2 |
∴
| tan(540°+x) |
| tan(900°-x) |
| sin(-x) |
| sin(450°-x) |
| cos(360°-x) |
| tan(-x) |
| tanx |
| (-tanx) |
| (-sinx) |
| cosx |
| cosx |
| (-tanx) |
| ||
| 2 |
点评:本题主要考查任意角的三角函数的定义,两点间的距离公式的应用,属于基础题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
 在植物活动前为保证树苗的质量,林管部门会对树苗进行检测.先从甲、乙两种树苗中各抽测了10株树苗的高度,量出的高度(单位:厘米)制作成茎叶图如下,甲,乙两种树苗的平均高度分别记为
在植物活动前为保证树苗的质量,林管部门会对树苗进行检测.先从甲、乙两种树苗中各抽测了10株树苗的高度,量出的高度(单位:厘米)制作成茎叶图如下,甲,乙两种树苗的平均高度分别记为| x |
| y |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设等差数列{an}的前n项和为Sn,若2a8=6+a11,则S9的值等于( )
| A、36 | B、45 | C、54 | D、27 |
不等式ax2-(a+2)x+2≥0(a<0)的解集为( )
A、[
| ||
B、[1,
| ||
C、(-∞,
| ||
D、(-∞,1]∪[
|
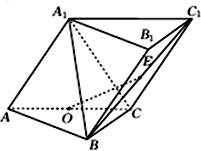 如图,三棱柱ABC-A1 B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,AB=BC且AB⊥BC,O为AC中点.
如图,三棱柱ABC-A1 B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,AB=BC且AB⊥BC,O为AC中点.