题目内容
设f(x)是定义在R上且周期为2的函数,在区间(-1,1]上,f(x)=
.其中常数a∈R,且f(
)=f(
).
(1)求a的值;
(2)设函数g(x)=f(x)+f(-x),x∈[-2,-1]∪[1,2].
①求证:g(x)是偶函数;
②求函数g(x)的值域.
|
| 1 |
| 2 |
| 3 |
| 2 |
(1)求a的值;
(2)设函数g(x)=f(x)+f(-x),x∈[-2,-1]∪[1,2].
①求证:g(x)是偶函数;
②求函数g(x)的值域.
考点:函数的周期性,分段函数的应用
专题:函数的性质及应用
分析:(1)由已知条件推导出f(
)=
,f(
)=f(
)=
=0,由此能求出a=-4.
(2)由g(-x)=f(-x)+f(-(-x))=f(-x)+f(x)=g(x),能证明g(x)是偶函数.
②由函数g(x)的值域与函数g(x)在[1.2]上的值域相等,求出g(1)=-2,g(2)=4,从而得到g(x)=2x-
-7,利用导数求出g(x)在(1,2)内是增函数,由此能求出函数g(x)的值域.
| 1 |
| 2 |
| a+4 |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
| a+4 |
| 3 |
(2)由g(-x)=f(-x)+f(-(-x))=f(-x)+f(x)=g(x),能证明g(x)是偶函数.
②由函数g(x)的值域与函数g(x)在[1.2]上的值域相等,求出g(1)=-2,g(2)=4,从而得到g(x)=2x-
| 6 |
| x-3 |
解答:
(1)解:f(
)=
=
,…(1分)
由函数f(x)的周期为2,
得f(
)=f(
-2)=f(-
)=2(-
)+1=0,…(3分)
∵f(
)=f(
),∴
=0,解得a=-4.…(4分)
(2)①证明:∵对?x∈[-2,-1]∪[1,2],有-x∈[-2,-1]∪[1,2],
且g(-x)=f(-x)+f(-(-x))=f(-x)+f(x)=g(x),
∴g(x)是偶函数.…(6分)
②解:由①知函数g(x)的值域与函数g(x)在[1.2]上的值域相等,
g(1)=f(1)+f(-1)=f(1)+f(-1+2)=2f(1)=-2,
g(2)=f(2)+f(-2)=2f(0)=4,…(8分)
当1<x<2时,-2<-x<-1,g(x)=f(x)+f(-x)=f(x-2)+(-x+2),
g(x)=2(x-2)+1+
=2x-
-7,…(10分)
g′(x)=2+
>0,g(x)在(1,2)内是增函数,…(11分)
得2-
-7<g(x)<2×2-
-7,即-2<g(x)<3,…(13分)
综上知,函数g(x)的值域为[-2,3)∪{4}.…(14分)
| 1 |
| 2 |
| ||
|
| a+4 |
| 3 |
由函数f(x)的周期为2,
得f(
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵f(
| 1 |
| 2 |
| 3 |
| 2 |
| a+4 |
| 3 |
(2)①证明:∵对?x∈[-2,-1]∪[1,2],有-x∈[-2,-1]∪[1,2],
且g(-x)=f(-x)+f(-(-x))=f(-x)+f(x)=g(x),
∴g(x)是偶函数.…(6分)
②解:由①知函数g(x)的值域与函数g(x)在[1.2]上的值域相等,
g(1)=f(1)+f(-1)=f(1)+f(-1+2)=2f(1)=-2,
g(2)=f(2)+f(-2)=2f(0)=4,…(8分)
当1<x<2时,-2<-x<-1,g(x)=f(x)+f(-x)=f(x-2)+(-x+2),
g(x)=2(x-2)+1+
| -4(2-x)+2 |
| (2-x)+1 |
=2x-
| 6 |
| x-3 |
g′(x)=2+
| 6 |
| (x-3)2 |
得2-
| 6 |
| 1-3 |
| 6 |
| 2-3 |
综上知,函数g(x)的值域为[-2,3)∪{4}.…(14分)
点评:本题考查实数值的求法,考查偶函数的证明,考查函数的值域的求法,解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
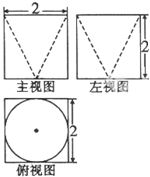
某几何体的三视图如图所示,则它的表面积是( )

A、24+
| ||
| B、24-π | ||
C、24+(
| ||
D、20+(
|
已知一个几何体的正视图是直径为2的圆,侧视图、俯视图都是边长为2的正方形,则该几何体的体积为( )
| A、2π | B、4π | C、6π | D、8π |
某几何体的三视图如图所示,则该几何体的体积为( )


| A、8π+16 | B、8π-16 |
| C、8π+8 | D、16π-8 |