题目内容

设F1，F2分别是双曲线
x2
a2
-
y2
b2
=1的左、右焦点．若双曲线上存在点M，使∠F1MF2=60°，且|MF1|=2|MF2|，则双曲线离心率为（　　）
A、
2
B、
3
C、2
D、
5
考点：双曲线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：由双曲线的定义知|MF1|=4a，|MF2|=2a，由余弦定理得c=
3
a，由此能求出双曲线的离心率．
解答： 解：∵点M在双曲线
x2
a2
-
y2
b2
=1上，且|MF1|=2|MF2|，
∴由双曲线的定义知|MF1|=4a，|MF2|=2a，
又∵∠F1MF2=60°，
∴在△MF1F2中，由余弦定理得16a2+4a2-2•4a•2a•cos60°=4c2，
解得c=
3
a，∴e=
c
a
=
3
．
故选：B．
点评：本题考查双曲线的离心率的求法，是中档题，解题时要认真审题，注意余弦定理的合理运用．
练习册系列答案
相关题目
给出下列四个命题：
①已知椭圆
x2
16
+
y2
9
=1的左右焦点分别为F1，F2，P为椭圆上一点，并且|PF1|=3，则|PF2|=1；
②双曲线C：
y2
9
-
x2
16
=1的顶点到渐近线的距离为
12
5
；
③若⊙C1：x2+y2+2x=0；⊙C2：x2+y2+2y-1=0，则这两圆恰有2条公切线；
④若直线l1：a2x-y+6=0与直线l2：4x-（a-3）y+9=0互相垂直，则a=-1
其中正确命题的序号是
 
．（把你认为正确命题的序号都填上）
在△ABC中，已知∠A满足：
3
sinA+cosA=1，AB=2，AC=3，则边BC的长为
 
．
已知f（n）（x）是对函数f（x）连续进行n次求导，若f（x）=x6+x5，对于任意x∈R，都有f（n）（x）=0，则n的最小值为
 
．
已知
e1
=
a
+5
b
，
e2
=3
a
-2
b
，
e3
=-6
a
+4
b
，
a
与
b
不共线，其中共线的是（　　）
A、
e1
与
e2
B、
e2
与
e3
C、
e1
与
e3
D、
e1
、
e2
、
e3
两两不共线
已知中心在坐标原点，焦点在坐标轴上的双曲线的渐近线方程为y=±
3
4
x则该双曲线的离心率为（　　）
A、
5
4
B、
5
3
C、
5
4
或
5
3
D、
3
5
或
4
5
已知正项等比数列{an}满足：a2013=a2012+2a2011，且
an•am
=4a1，则6（
1
m
+
1
n
）的最小值为（　　）
A、4
B、2
C、
2
3
D、6
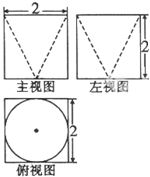
某几何体的三视图如图所示，则它的表面积是（　　）
A、24+
5
π
B、24-π
C、24+(
5
-1)π
D、20+(
5
-1)π
已知一个几何体的正视图是直径为2的圆，侧视图、俯视图都是边长为2的正方形，则该几何体的体积为（　　）
A、2πB、4πC、6πD、8π

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网