题目内容
20.若$\frac{cosx-sinx}{cosx+sinx}$=2,则sin2x-sin2x=$\frac{7}{10}$.分析 根据条件得出sinx,cosx的关系,利用sin2x+cos2x=1解出cos2x,代入式子计算即可.
解答 解:∵$\frac{cosx-sinx}{cosx+sinx}$=2,∴sinx=-$\frac{1}{3}$cosx.
∵sin2x+cos2x=1,∴$\frac{1}{9}co{s}^{2}x$+cos2x=1,解得cos2x=$\frac{9}{10}$.
∴sin2x-sin2x=$\frac{1}{9}$cos2x-2sinxcosx=$\frac{1}{9}co{s}^{2}x$+$\frac{2}{3}co{s}^{2}x$=$\frac{7}{9}$cos2x=$\frac{7}{10}$.
故答案为:$\frac{7}{10}$.
点评 本题考查了同角三角函数的关系,三角函数的恒等变换与化简求值,属于基础题.

练习册系列答案
相关题目
5.在二项式(3+2x)8的展开式中,最大的二项式系数是( )
| A. | C${\;}_{8}^{3}$ | B. | ${C}_{8}^{4}$ | C. | ${C}_{8}^{5}$ | D. | ${C}_{8}^{6}$ |
4.等差数列{an}前n项和为Sn,且$\frac{{S}_{2016}}{2016}$=$\frac{{S}_{2015}}{2015}$+1,则数列{an}的公差为( )
| A. | 1 | B. | 2 | C. | 2015 | D. | 2016 |
2.若2sin2α=1-cos2α,则tanα等于( )
| A. | -2 | B. | 2 | C. | -2或0 | D. | 2或0 |
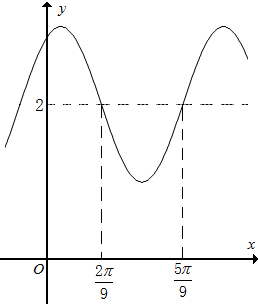 函数y=Asin(ωx+φ)+2(A>0,ω>0,0<φ<2π)的图象如图所示,则ω=3,φ=$\frac{π}{3}$.
函数y=Asin(ωx+φ)+2(A>0,ω>0,0<φ<2π)的图象如图所示,则ω=3,φ=$\frac{π}{3}$.