题目内容
2．若2sin2α=1-cos2α，则tanα等于（ ）| A． | -2 | B． | 2 | C． | -2或0 | D． | 2或0 |
分析 由条件利用二倍角公式、同角三角函数的基本关系，求得tanα的值．
解答 解：∵2sin2α=1-cos2α，即4sinαcosα=1-（1-2sin2α）=2sin2α，
∴sinα=0 或2cosα=sinα，∴tanα=0 或tanα=2，
故选：D．
点评 本题主要考查二倍角公式的应用，同角三角函数的基本关系，属于基础题．
练习册系列答案
一线名师提优试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
13．
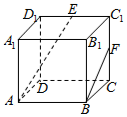如图，在正方体ABCD-A1B1C1D1中，E，F分别是C1D1，CC1的中点，则异面直线AE与BF所成角的余弦值为（ ）
如图，在正方体ABCD-A1B1C1D1中，E，F分别是C1D1，CC1的中点，则异面直线AE与BF所成角的余弦值为（ ）| A． | -$\frac{{5\sqrt{6}}}{18}$ | B． | -$\frac{{\sqrt{5}}}{5}$ | C． | $\frac{{\sqrt{6}}}{5}$ | D． | $\frac{{2\sqrt{5}}}{5}$ |
如图，△ABC是边长为2的等边三角形，△ABD是等腰直角三角形，AD⊥BD，平面ABC⊥平面ABD，且EC⊥平面ABC，EC=1．