题目内容
1.若圆锥的侧面展开图是半径为1cm、圆心角为120°的扇形,则这个圆锥的轴截面面积等于$\frac{2\sqrt{2}}{9}$.分析 根据圆锥侧面展开图与圆锥的对应关系列方程解出圆锥的底面半径和母线长,计算出圆锥的高.
解答 解:设圆锥的底面半径为r,母线长为l,则$\left\{\begin{array}{l}{l=1}\\{2πr=\frac{2π}{3}×1}\end{array}\right.$,
解得l=1,r=$\frac{1}{3}$.
∴圆锥的高h=$\sqrt{{l}^{2}-{r}^{2}}$=$\frac{2\sqrt{2}}{3}$.
∴圆锥的轴截面面积S=$\frac{1}{2}×2r×h$=$\frac{2\sqrt{2}}{9}$.
故答案为:$\frac{2\sqrt{2}}{9}$.
点评 本题考查了圆锥的结构特征,弧长公式,属于基础题.

练习册系列答案
相关题目
9.已知正数x,y,z满足5x+4y+3z=10,则${9^{x^2}}+{9^{{y^2}+{z^2}}}$的最小值为( )
| A. | 27 | B. | 18 | C. | 36 | D. | 54 |
13.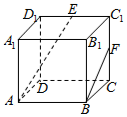 如图,在正方体ABCD-A1B1C1D1中,E,F分别是C1D1,CC1的中点,则异面直线AE与BF所成角的余弦值为( )
如图,在正方体ABCD-A1B1C1D1中,E,F分别是C1D1,CC1的中点,则异面直线AE与BF所成角的余弦值为( )
 如图,在正方体ABCD-A1B1C1D1中,E,F分别是C1D1,CC1的中点,则异面直线AE与BF所成角的余弦值为( )
如图,在正方体ABCD-A1B1C1D1中,E,F分别是C1D1,CC1的中点,则异面直线AE与BF所成角的余弦值为( )| A. | -$\frac{{5\sqrt{6}}}{18}$ | B. | -$\frac{{\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{6}}}{5}$ | D. | $\frac{{2\sqrt{5}}}{5}$ |
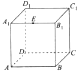 如图,正方体ABCD-A1B1C1D1的棱长为1,E为A1B1的中点,则下列五个命题:
如图,正方体ABCD-A1B1C1D1的棱长为1,E为A1B1的中点,则下列五个命题: 如图,△ABC是边长为2的等边三角形,△ABD是等腰直角三角形,AD⊥BD,平面ABC⊥平面ABD,且EC⊥平面ABC,EC=1.
如图,△ABC是边长为2的等边三角形,△ABD是等腰直角三角形,AD⊥BD,平面ABC⊥平面ABD,且EC⊥平面ABC,EC=1.