题目内容
10.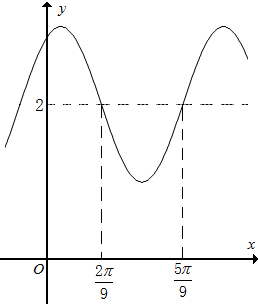 函数y=Asin(ωx+φ)+2(A>0,ω>0,0<φ<2π)的图象如图所示,则ω=3,φ=$\frac{π}{3}$.
函数y=Asin(ωx+φ)+2(A>0,ω>0,0<φ<2π)的图象如图所示,则ω=3,φ=$\frac{π}{3}$.
分析 首先根据函数的图象得到最小正周期T,进而根据周期公式可求ω,再根据平衡点利用五点作图法求出φ,即可得解.
解答 解:∵由函数图象可知,T=2($\frac{5π}{9}$-$\frac{2π}{9}$)=$\frac{2π}{3}$,
∴ω=$\frac{2π}{T}$=3,
∵函数图象过点($\frac{2π}{9}$,2),
∴Asin(3×$\frac{2π}{9}$+φ)+2=2,由五点法作图可得:3×$\frac{2π}{9}$+φ=π,
∴解得:φ=$\frac{π}{3}$.
故答案为:3,$\frac{π}{3}$.
点评 解决此类问题的关键是求φ,首先根据函数的图象得到ω,再根据最值点或者平衡点求出所有的φ,进而根据φ的范围求出答案即可,注意在代入已知点时最好代入最值点,因为在一个周期内只有一个最大值,一个最小值,而平衡点却有两个,假如代入的是平衡点则需要根据函数的单调性再来判定φ的取值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.函数y=sin($\frac{2015}{2}$π-x)是( )
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 非奇非偶函数 | D. | 既是奇函数又是偶函数 |
18.在某项测量中,测量结果X服从正态分布N(2,σ2)(σ>0),若X在(0,2)内取值的概率为0.4,则X在(-∞,4)内取值的概率为( )
| A. | 0.1 | B. | 0.2 | C. | 0.8 | D. | 0.9 |
5.已知命题P:“若b2=ac(a,b,c∈R),则a,b,c成等比数列”,q:“函数f(x)=cos($\frac{π}{2}$+x)是奇函数”,则下列命题为真命题的是( )
| A. | p∨q | B. | p∧q | C. | p∨¬q | D. | ¬p∧¬q |