题目内容
4．等差数列{an}前n项和为Sn，且$\frac{{S}_{2016}}{2016}$=$\frac{{S}_{2015}}{2015}$+1，则数列{an}的公差为（ ）| A． | 1 | B． | 2 | C． | 2015 | D． | 2016 |
分析 设等差数列{an}的公差为d．可得$\frac{{S}_{n+1}}{n+1}-\frac{{S}_{n}}{n}$=$\frac{{a}_{n+1}-{a}_{n}}{2}$=$\frac{1}{2}$d，即可得出．
解答 解：设等差数列{an}的公差为d．
∵${S}_{n}=\frac{n（{a}_{1}+{a}_{n}）}{2}$，
∴$\frac{{S}_{n+1}}{n+1}-\frac{{S}_{n}}{n}$=$\frac{{a}_{1}+{a}_{n+1}}{2}$-$\frac{{a}_{1}+{a}_{n}}{2}$=$\frac{{a}_{n+1}-{a}_{n}}{2}$=$\frac{1}{2}$d
又$\frac{{S}_{2016}}{2016}$=$\frac{{S}_{2015}}{2015}$+1，
∴等差数列{an}的公差为2．
故选：B．
点评 本题考查了递推关系、等差数列的通项公式及其前n项和公式及其性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
3．某学校组织的数学赛中，学生的竞赛成绩X服从正态分布X～N（100，σ2），P（X＞120）=a，P（80≤X≤100）=b，则$\frac{4}{a}$+$\frac{1}{b}$的最小值为（ ）
| A． | 8 | B． | 9 | C． | 16 | D． | 18 |
9．已知正数x，y，z满足5x+4y+3z=10，则${9^{x^2}}+{9^{{y^2}+{z^2}}}$的最小值为（ ）
| A． | 27 | B． | 18 | C． | 36 | D． | 54 |
13．
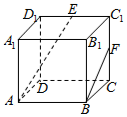如图，在正方体ABCD-A1B1C1D1中，E，F分别是C1D1，CC1的中点，则异面直线AE与BF所成角的余弦值为（ ）
如图，在正方体ABCD-A1B1C1D1中，E，F分别是C1D1，CC1的中点，则异面直线AE与BF所成角的余弦值为（ ）| A． | -$\frac{{5\sqrt{6}}}{18}$ | B． | -$\frac{{\sqrt{5}}}{5}$ | C． | $\frac{{\sqrt{6}}}{5}$ | D． | $\frac{{2\sqrt{5}}}{5}$ |