题目内容
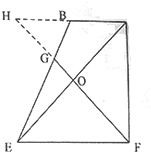
 如图,三棱台ABC-DEF中,CF⊥平面DEF,AB⊥BC.
如图,三棱台ABC-DEF中,CF⊥平面DEF,AB⊥BC.(Ⅰ)设平面AEC∩平面DEF=a,求证DF∥a;
(Ⅱ)若EF=CF=2BC,试同在线段BE上是否存在点G,使得平面DFG⊥平面CDE,若存在,请确定G点的位置;若不存在,说明理由.
考点:直线与平面垂直的性质,直线与平面平行的性质
专题:空间位置关系与距离
分析:(Ⅰ)由已知条件得AC∥DF,所以DF∥平面ACE,由此能证明DF∥a.
(Ⅱ)线段BE上存在点G,且BG=
BE,使得平面DFG⊥平面CDE.利用三角形全等和三角形相似进行证明.
(Ⅱ)线段BE上存在点G,且BG=
| 1 |
| 3 |
解答:
 (Ⅰ)证明:在三棱台ABC-DEF中,AC∥DF,
(Ⅰ)证明:在三棱台ABC-DEF中,AC∥DF,
∵AC?平面ACE,DF?平面ACE,
∴DF∥平面ACE,
∵DF?平面DEF,平面ACE∩平面DEF=a,
∴DF∥a.
(Ⅱ)解:线段BE上存在点G,且BG=
BE,使得平面DFG⊥平面CDE,
证明如下:
取CE中点O,连结FO并延长交BE于点G,连结GD、GF,
∵CF=EF,∴GF⊥CE,
在三棱台ABC-DEF中,AB⊥BC,∴DE⊥EF,
由CF⊥平面DEF,得CF⊥DE,又CF∩EF=F,
∴DE⊥平面DEF,∴DE⊥GF,
∵GF⊥CE,GF⊥DE,CE∩DE=E,∴GF⊥平面CDE,
又GF?平面DFG,∴平面DFG⊥平面CDE,
此时,如平面图所示,∵O为CE中点,CF=EF=2BC,
由平面几何知识,得△HOC≌△FOE,
∴HB=BC=
EF,
由△HGB∽△FOE,得
=
,
∴BG=
BE.
 (Ⅰ)证明:在三棱台ABC-DEF中,AC∥DF,
(Ⅰ)证明:在三棱台ABC-DEF中,AC∥DF,∵AC?平面ACE,DF?平面ACE,
∴DF∥平面ACE,
∵DF?平面DEF,平面ACE∩平面DEF=a,
∴DF∥a.
(Ⅱ)解:线段BE上存在点G,且BG=
| 1 |
| 3 |
证明如下:
取CE中点O,连结FO并延长交BE于点G,连结GD、GF,
∵CF=EF,∴GF⊥CE,
在三棱台ABC-DEF中,AB⊥BC,∴DE⊥EF,
由CF⊥平面DEF,得CF⊥DE,又CF∩EF=F,
∴DE⊥平面DEF,∴DE⊥GF,
∵GF⊥CE,GF⊥DE,CE∩DE=E,∴GF⊥平面CDE,
又GF?平面DFG,∴平面DFG⊥平面CDE,
此时,如平面图所示,∵O为CE中点,CF=EF=2BC,
由平面几何知识,得△HOC≌△FOE,
∴HB=BC=
| 1 |
| 2 |
由△HGB∽△FOE,得
| BG |
| GE |
| 1 |
| 2 |
∴BG=
| 1 |
| 3 |
点评:本题考查直线与直线垂直的证明,考查使得面面垂直的点是否存在的判断与证明,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
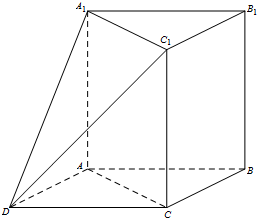 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=90°.以AB,BC为邻边作平行四边形ABCD,连接DA1和DC1.
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=90°.以AB,BC为邻边作平行四边形ABCD,连接DA1和DC1. 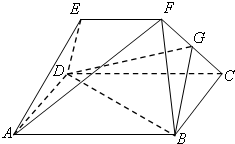 如图几何体中,四边形ABCD为矩形,AB=2BC=4,BF=CF=AE=DE,EF=2,EF∥AB,AF⊥CF.
如图几何体中,四边形ABCD为矩形,AB=2BC=4,BF=CF=AE=DE,EF=2,EF∥AB,AF⊥CF.