题目内容
已知(3
-
)n的展开式中各项系数之和为256,则展开式中第7项的系数是 .
| 3 | x2 |
| 1 | ||
|
考点:二项式系数的性质
专题:二项式定理
分析:令x=1可得各项系数之和,再根据各项系数之和为256,求得n的值,再根据二项式展开式的通项公式,求得展开式中第7项的系数.
解答:
解:(3
-
)n的展开式中,令x=1可得各项系数之和为(3-1)n=256,求得n=8,
则(3
-
)n =(3
-
)8的展开式中第7项是 T7=
•3•(-1)7•x-
=-24x-
,
故展开式中第7项的系数是-24,
故答案为:-24.
| 3 | x2 |
| 1 | ||
|
则(3
| 3 | x2 |
| 1 | ||
|
| 3 | x2 |
| 1 | ||
|
| C | 7 8 |
| 17 |
| 6 |
| 17 |
| 6 |
故展开式中第7项的系数是-24,
故答案为:-24.
点评:本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,求展开式中某项的系数,属于基础题.

练习册系列答案
相关题目
 如图,三棱台ABC-DEF中,CF⊥平面DEF,AB⊥BC.
如图,三棱台ABC-DEF中,CF⊥平面DEF,AB⊥BC.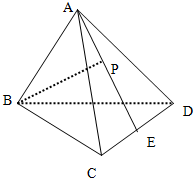 已知空间四边形ABCD,BC=BD,AC=AD,E是CD边的中点.在AE上的一个动点P,讨论BP与CD是否存在垂直关系,并证明你的结论.
已知空间四边形ABCD,BC=BD,AC=AD,E是CD边的中点.在AE上的一个动点P,讨论BP与CD是否存在垂直关系,并证明你的结论.