题目内容
调查某家具厂油漆工患某种皮肤病情况,结果如下表:
(Ⅰ)请将2×2列联表中的数据补充完整;
(Ⅱ)利用2×2列联表的独立性检验估计,能够以99%的把握认为“患该皮肤病与是否为油漆工”有关吗?为什么?
| 工种 健康状况 |
非油漆工 | 油漆工 | 合计 |
| 健康人数 | 28 | ||
| 患病人数 | 2 | 8 | |
| 合计 | 40 |
(Ⅱ)利用2×2列联表的独立性检验估计,能够以99%的把握认为“患该皮肤病与是否为油漆工”有关吗?为什么?
考点:独立性检验的应用
专题:应用题,概率与统计
分析:(1)根据所给的数据,得到列联表.
(2)把列联表中的数据代入求观测值的公式,求出这组数据的观测值,把观测值同临界值进行比较,得到有99%的把握认为“患该皮肤病与是否为油漆工”有关.
(2)把列联表中的数据代入求观测值的公式,求出这组数据的观测值,把观测值同临界值进行比较,得到有99%的把握认为“患该皮肤病与是否为油漆工”有关.
解答:
解:(Ⅰ)
(2)K2=
≈21.5>6.635,
∴有99%的把握认为“患该皮肤病与是否为油漆工”有关.
| 工种 健康状况 |
非油漆工 | 油漆工 | 合 计 |
| 健康人数 | 28 | 2 | 30 |
| 患病人数 | 2 | 8 | 10 |
| 合 计 | 30 | 10 | 40 |
| 40(28×8-2×2)2 |
| 30×10×30×10 |
∴有99%的把握认为“患该皮肤病与是否为油漆工”有关.
点评:本题考查独立性检验的应用,本题解题的关键是正确读图和作图,正确理解临界值对应的概率的意义,本题是一个基础题.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
已知(1-2x)2014=a0+a1x+a2x2+…+a2014x2014,则a0+a1+a2+…+a2014=( )
| A、22014 |
| B、32013 |
| C、1 |
| D、-1 |
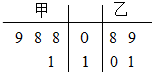 甲、乙两名运动员在4次训练中的得分情况如下面的茎叶图所示.
甲、乙两名运动员在4次训练中的得分情况如下面的茎叶图所示. 如图,三棱台ABC-DEF中,CF⊥平面DEF,AB⊥BC.
如图,三棱台ABC-DEF中,CF⊥平面DEF,AB⊥BC.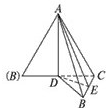 如图,等边△ABC的边长为1,BC边上的高为AD,若沿AD折成直二面角,求二面角A-BC-D的正切值.
如图,等边△ABC的边长为1,BC边上的高为AD,若沿AD折成直二面角,求二面角A-BC-D的正切值.