题目内容
在△ABC中,角A,B,C的对边长分别为a,b,c,已知向量
=(2cos
,sin
),
=(cos
,2sin
),
•
=-1.
(1)求角A的值;
(2)若a=2
,b=2,求c的值.
| m |
| A |
| 2 |
| A |
| 2 |
| n |
| A |
| 2 |
| A |
| 2 |
| m |
| n |
(1)求角A的值;
(2)若a=2
| 3 |
考点:正弦定理,平面向量数量积的运算
专题:解三角形
分析:(1)利用向量数量积的公式建立等式求得cosA的值,进而求得A.
(2)先由正弦定理求得sinB的值,进而求得B,最后利用三角形内角和求得C,得知C=B,进而求得c=b,则c可求得.
(2)先由正弦定理求得sinB的值,进而求得B,最后利用三角形内角和求得C,得知C=B,进而求得c=b,则c可求得.
解答:
解:(1)
•
=2cos2
-2sin2
=-1,
∴2cosA=-1,cosA=-
,
∵0<A<π,
∴A=
.
(2)由正弦定理知
=
,
∴sinB=
=
,
∵b<a,
∴B<A,
∴B=
,
∴C=π-A-B=
,
∴c=b=2.
| m |
| n |
| A |
| 2 |
| A |
| 2 |
∴2cosA=-1,cosA=-
| 1 |
| 2 |
∵0<A<π,
∴A=
| 2π |
| 3 |
(2)由正弦定理知
| a |
| sinA |
| b |
| sinB |
∴sinB=
| bsinA |
| a |
| 1 |
| 2 |
∵b<a,
∴B<A,
∴B=
| π |
| 6 |
∴C=π-A-B=
| π |
| 6 |
∴c=b=2.
点评:本题主要考查了正弦定理的应用,平面向量的数量积的运算.综合考查了学生对基础知识的运用.

练习册系列答案
相关题目
若存在x∈[-2,3],使不等式2x-x2≥a成立,则实数a的取值范围是( )
| A、(-∞,1] |
| B、(-∞,-8] |
| C、[1,+∞) |
| D、[-8,+∞) |
 如图,三棱台ABC-DEF中,CF⊥平面DEF,AB⊥BC.
如图,三棱台ABC-DEF中,CF⊥平面DEF,AB⊥BC.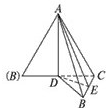 如图,等边△ABC的边长为1,BC边上的高为AD,若沿AD折成直二面角,求二面角A-BC-D的正切值.
如图,等边△ABC的边长为1,BC边上的高为AD,若沿AD折成直二面角,求二面角A-BC-D的正切值.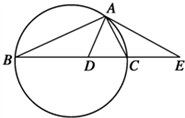 如图,设△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与
如图,设△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与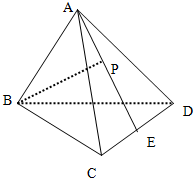 已知空间四边形ABCD,BC=BD,AC=AD,E是CD边的中点.在AE上的一个动点P,讨论BP与CD是否存在垂直关系,并证明你的结论.
已知空间四边形ABCD,BC=BD,AC=AD,E是CD边的中点.在AE上的一个动点P,讨论BP与CD是否存在垂直关系,并证明你的结论.