题目内容
已知命题p:实数x满足-2≤1-
≤2,命题q:实数x满足x2-2x+(1-m2)≤0(m>0),若?q是?p的充分不必要条件,求实数m的取值范围.
| x-1 |
| 3 |
考点:复合命题的真假
专题:简易逻辑
分析:先化简命题P,Q,再利用充分必要条件即可得出.
解答:
解:由-2≤1-
≤2,得-2≤x≤10,
∴记A={x|p}={x|-2≤x≤10}.
由x2-2x+1-m2≤0(m>0)得1-m≤x≤1+m,
记B={x|q}={x|1-m≤x≤1+m(m>0)}.
∵?q是?p的充分不必要条件,
∴P是q的充分不必要条件,即P⇒q且q推不出P,∴A?B,
要使A?B,又m>0,则只需
,
∴m≥9.
故所求实数m的取值范围是m≥9.
| x-1 |
| 3 |
∴记A={x|p}={x|-2≤x≤10}.
由x2-2x+1-m2≤0(m>0)得1-m≤x≤1+m,
记B={x|q}={x|1-m≤x≤1+m(m>0)}.
∵?q是?p的充分不必要条件,
∴P是q的充分不必要条件,即P⇒q且q推不出P,∴A?B,
要使A?B,又m>0,则只需
|
∴m≥9.
故所求实数m的取值范围是m≥9.
点评:本题考查了命题之间的关系、充分必要条件,考查了推理能力,属于基础题.

练习册系列答案
相关题目
函数y=2sin2x的图象的一条对称轴方程是( )
A、x=
| ||
B、x=
| ||
C、x=
| ||
D、x=
|
 如图,三棱台ABC-DEF中,CF⊥平面DEF,AB⊥BC.
如图,三棱台ABC-DEF中,CF⊥平面DEF,AB⊥BC.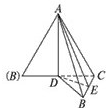 如图,等边△ABC的边长为1,BC边上的高为AD,若沿AD折成直二面角,求二面角A-BC-D的正切值.
如图,等边△ABC的边长为1,BC边上的高为AD,若沿AD折成直二面角,求二面角A-BC-D的正切值.