题目内容
已知f(x)=2x+3(x∈R),若|f(x)|<a的必要条件是|x+1|<b(a,b>0),则a,b之间的关系是( )
A、b≥
| ||
B、b<
| ||
C、a≤
| ||
D、a>
|
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据绝对值不等式的性质以及充分条件和必要条件的定义即可得到结论.
解答:
解:由|f(x)|<a得|2x+3|<a,
即
<x<
,
由|x+1|<b得-1-b<x<b-1.
若|f(x)|<a的必要条件是|x+1|<b(a,b>0),
则
.
即
.
即b≥
选A
即
| -3-a |
| 2 |
| a-3 |
| 2 |
由|x+1|<b得-1-b<x<b-1.
若|f(x)|<a的必要条件是|x+1|<b(a,b>0),
则
|
即
|
即b≥
| a+1 |
| 2 |
选A
点评:本题主要考查充分条件和必要条件的判断,根据绝对值不等式的性质是解决本题的关键.

练习册系列答案
相关题目
函数y=x|x|+px,x∈R是( )
| A、偶函数 |
| B、奇函数 |
| C、即不是奇函数也不是偶函数 |
| D、奇偶性与p有关 |
设a>0,且a≠1,且a≠2,则“函数y=logax在(0,+∞)上是减函数”是“函数y=(a-2)ax在R上是增函数”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
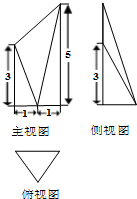 已知某几何体的三视图如图所示,其中俯视图是边长为2的正三角形,侧视图是直角三角形,则此几何体的体积为
已知某几何体的三视图如图所示,其中俯视图是边长为2的正三角形,侧视图是直角三角形,则此几何体的体积为