题目内容
设x、y≥0,且x2+y3≥x3+y4 ,求证:x3+y3≤2.
考点:不等式的证明
专题:证明题,不等式的解法及应用
分析:由于x、y≥0,且x2+y3≥x3+y4,即有x2(1-x)+y3(1-y)≥0,由于x≥0,y≥0,则1-x≥0,1-y≥0,即可得证.
解答:
证明:由于x、y≥0,且x2+y3≥x3+y4,
则有(x2-x3)+(y3-y4)≥0恒成立,
即有x2(1-x)+y3(1-y)≥0,
由于x≥0,y≥0,则1-x≥0,1-y≥0,
即有0≤x≤1,0≤y≤1,
则x3+y3≤2.
则有(x2-x3)+(y3-y4)≥0恒成立,
即有x2(1-x)+y3(1-y)≥0,
由于x≥0,y≥0,则1-x≥0,1-y≥0,
即有0≤x≤1,0≤y≤1,
则x3+y3≤2.
点评:本题考查不等式的证明,考查运用不等式的性质证明不等式,属于中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
函数y=x|x|+px,x∈R是( )
| A、偶函数 |
| B、奇函数 |
| C、即不是奇函数也不是偶函数 |
| D、奇偶性与p有关 |
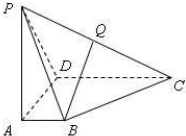 如图,四棱锥P-ABCD中,PA⊥底面ABCD,且PA=AB=AD=
如图,四棱锥P-ABCD中,PA⊥底面ABCD,且PA=AB=AD=| 1 |
| 2 |
(1)求证:PD⊥AB;
(2)在侧棱PC上是否存在一点Q,使BQ∥平面PAD?证明你的结论.
已知F是椭圆
+
=1(a>b>0)的右焦点,过点F作斜率为2的直线l使它与圆x2+y2=b2相切,则椭圆离心率是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
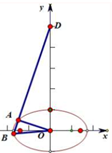 如图,椭圆方程x2+3y2=12,过D(0,10)直线l交椭圆于A、B两点,若OAB为直角三角形,求直线l方程.
如图,椭圆方程x2+3y2=12,过D(0,10)直线l交椭圆于A、B两点,若OAB为直角三角形,求直线l方程.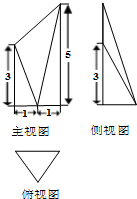 已知某几何体的三视图如图所示,其中俯视图是边长为2的正三角形,侧视图是直角三角形,则此几何体的体积为
已知某几何体的三视图如图所示,其中俯视图是边长为2的正三角形,侧视图是直角三角形,则此几何体的体积为