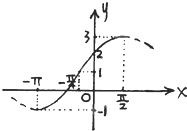
题目内容
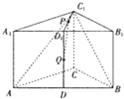 如图,在正三棱柱ABC-A1B1C1中,底面边长为2,侧棱长为
如图,在正三棱柱ABC-A1B1C1中,底面边长为2,侧棱长为| 2 |
(Ⅰ)求证:PQ∥平面ABC1;
(Ⅱ)求三棱锥Q-ABC1的体积.
考点:直线与平面平行的判定,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(Ⅰ)连接C1D,利用中位线的性质证明出PQ∥C1D,进而根据线面平行的判定定理证明出PQ∥平面ABC1.
(Ⅱ)利用等体积法先求得几何体C1-ABQ,通过求得底面ABQ的面积,最后利用体积公式求得答案.
(Ⅱ)利用等体积法先求得几何体C1-ABQ,通过求得底面ABQ的面积,最后利用体积公式求得答案.
解答:
(Ⅰ)证明:连接C1D,
∵P,Q分别为C1D1,DD1中点,
∴PQ∥C1D,
∵PQ?平面ABC1,C1D?平面ABC1,
∴PQ∥平面ABC1.
(Ⅱ)VQ-ABC1=VC1-ABQ=
S△ABQ•C1D1,
∵在△A1B1C1中,C1D1=
A1B1=
,
S△ABQ=
AB•DQ=
×2×
=
,
∴VQ-ABC1=
×
×
=
.
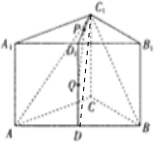
∵P,Q分别为C1D1,DD1中点,
∴PQ∥C1D,
∵PQ?平面ABC1,C1D?平面ABC1,
∴PQ∥平面ABC1.
(Ⅱ)VQ-ABC1=VC1-ABQ=
| 1 |
| 3 |
∵在△A1B1C1中,C1D1=
| ||
| 2 |
| 3 |
S△ABQ=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
∴VQ-ABC1=
| 1 |
| 3 |
| ||
| 2 |
| 3 |
| ||
| 6 |

点评:本题主要考查了线面平行的判定定理的应用,棱柱的体积的计算.考查了学生综合分析的能力和观察能力.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案
相关题目
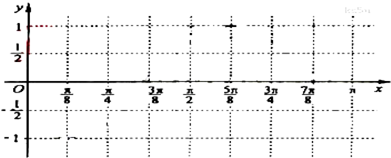
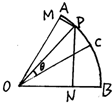 如图,扇形OAB的半径为2,圆心角为
如图,扇形OAB的半径为2,圆心角为