题目内容
已知双曲线C1:
-
=1,点A、B分别为双曲线C1的左、右焦点,动点C在x轴上方.
(1)若点C的坐标为C(x0,3)(x0>0)是双曲线的一条渐近线上的点,求以A、B为焦点且经过点C的椭圆的方程;
(2)若∠ACB=45°,求△ABC的外接圆的方程;
(3)若在给定直线y=x+t上任取一点P,从点P向(2)中圆引一条切线,切点为Q.问是否存在一个定点M,恒有|PM|=|PQ|?请说明理由.
| 13x2 |
| 16 |
| 13y2 |
| 36 |
(1)若点C的坐标为C(x0,3)(x0>0)是双曲线的一条渐近线上的点,求以A、B为焦点且经过点C的椭圆的方程;
(2)若∠ACB=45°,求△ABC的外接圆的方程;
(3)若在给定直线y=x+t上任取一点P,从点P向(2)中圆引一条切线,切点为Q.问是否存在一个定点M,恒有|PM|=|PQ|?请说明理由.
考点:直线与圆锥曲线的关系,椭圆的标准方程
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:(1)求出双曲线C1的左、右焦点A、B的坐标和渐进线方程,由定义求出椭圆的长轴长,半焦距c,及b,即可得到椭圆方程;
(2)运用正弦定理
=2R得到R=2
,又圆心在线段AB的垂直平分线上,求出圆心,即可得到圆的方程;
(3)假设存在这样的定点M(m,n),设点P的坐标为(x,x+t)由恒有|PM|=|PQ|,运用两点的距离公式和切线长公式,化简得到(2m+2n-4)x-(m2+n2-2nt+4t+4)=0对x∈R恒成立.令系数为0,再消去m,由判别式的符号,即可判断.
(2)运用正弦定理
| |AB| |
| sinC |
| 2 |
(3)假设存在这样的定点M(m,n),设点P的坐标为(x,x+t)由恒有|PM|=|PQ|,运用两点的距离公式和切线长公式,化简得到(2m+2n-4)x-(m2+n2-2nt+4t+4)=0对x∈R恒成立.令系数为0,再消去m,由判别式的符号,即可判断.
解答:
解:(1)双曲线C1的左、右焦点A、B的坐标分别为(-2,0)和(2,0),
∵双曲线的渐进线方程为:y=±
x,
∴点C的坐标为(x0,3)(x0>0)是渐进线y=
x上的点,即点C的坐标为(2,3).
∵|AC|=5,|BC|=3∴椭圆的长轴长2a=|AC|+|BC|=8>|AB|=4,
∵半焦距c=2,∴b2=a2-c2=16-4=12.
∴椭圆的方程为
+
=1;
(2)∵
=2R,∴2R=4
,即R=2
又圆心在线段AB的垂直平分线上,故可设圆心(0,s)(s>0)
由4+s2=8,s=2.∴△ABC的外接圆的方程为x2+(y-2)2=8;
(3)假设存在这样的定点M(m,n),设点P的坐标为(x,x+t)
∵恒有|PM|=|PQ|,∴(x-m)2+(x+t-n)2=x2+(x+t-2)2-8
即(2m+2n-4)x-(m2+n2-2nt+4t+4)=0对x∈R恒成立.
从而2m+2n-4=0且m2+n2-2nt+4t+4=0,消去m,得n2-(t+2)n+(2t+4)=0①
∵方程①的判别式△=t2-4t-12
∴①当-2<t<6时,方程①无实数解,∴不存在这样的定点M;
②当t≤-2或t≥6时,方程①有实数解,此时
≥2
,即直线y=x+t与圆相离或相切,
故此时存在这样的定点M.
∵双曲线的渐进线方程为:y=±
| 3 |
| 2 |
∴点C的坐标为(x0,3)(x0>0)是渐进线y=
| 3 |
| 2 |
∵|AC|=5,|BC|=3∴椭圆的长轴长2a=|AC|+|BC|=8>|AB|=4,
∵半焦距c=2,∴b2=a2-c2=16-4=12.
∴椭圆的方程为
| x2 |
| 16 |
| y2 |
| 12 |
(2)∵
| |AB| |
| sinC |
| 2 |
| 2 |
又圆心在线段AB的垂直平分线上,故可设圆心(0,s)(s>0)
由4+s2=8,s=2.∴△ABC的外接圆的方程为x2+(y-2)2=8;
(3)假设存在这样的定点M(m,n),设点P的坐标为(x,x+t)
∵恒有|PM|=|PQ|,∴(x-m)2+(x+t-n)2=x2+(x+t-2)2-8
即(2m+2n-4)x-(m2+n2-2nt+4t+4)=0对x∈R恒成立.
从而2m+2n-4=0且m2+n2-2nt+4t+4=0,消去m,得n2-(t+2)n+(2t+4)=0①
∵方程①的判别式△=t2-4t-12
∴①当-2<t<6时,方程①无实数解,∴不存在这样的定点M;
②当t≤-2或t≥6时,方程①有实数解,此时
| |0-2+t| | ||
|
| 2 |
故此时存在这样的定点M.
点评:本题考查椭圆、双曲线的方程、定义和性质,考查圆的方程的求法,切线长的求法,考查定点问题,以及化简运算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
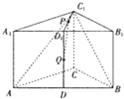 如图,在正三棱柱ABC-A1B1C1中,底面边长为2,侧棱长为
如图,在正三棱柱ABC-A1B1C1中,底面边长为2,侧棱长为