题目内容
已知集合A={x|x2-x≤0，x∈R}，设函数f（x）=2x2-2x+3，x∈A的值域为B，求集合B．
考点：指数函数综合题
专题：函数的性质及应用
分析：先把集合A解出来，再求函数f（x）=2x2-2x+3的值域．
解答：
解：∵A={x|x2-x≤0，x∈R}=[0，1]，…（3分）
因为：x2-2x+3=（x-1）2+2，
x2-2x+3∈[2，3]，
∴22x2-2x+3∈[4，8]，
∴B=[4，8]．…（12分）
因为：x2-2x+3=（x-1）2+2，
x2-2x+3∈[2，3]，
∴22x2-2x+3∈[4，8]，
∴B=[4，8]．…（12分）
点评：本题主要考查指数函数的性质，集合的关系，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
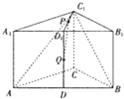如图，在正三棱柱ABC-A1B1C1中，底面边长为2，侧棱长为
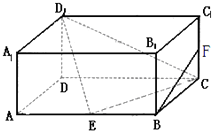如图，在长方体ABCD-A1B1C1D1中，AD=AA1=1，AB=2，E为AB的中点，F为CC1的中点．