题目内容
若(3x+1)n(n∈N*)的展开式中各项系数的和是256,则展开式中x2项的系数是 .
考点:二项式定理的应用
专题:二项式定理
分析:根据展开式中各项系数的和求出n的值,再由通项公式Tr+1求出展开式中x2项的系数.
解答:
解:根据题意,展开式中各项系数的和是
(3+1)n=256,
∴n=4;
该二项式的通项公式是
Tr+1=
•(3x)r•14-r,
令r=2,得:
•(3x)2=
•9•x2=54x2;
∴展开式中x2项的系数是54.
故答案为:54.
(3+1)n=256,
∴n=4;
该二项式的通项公式是
Tr+1=
| C | r 4 |
令r=2,得:
| C | 2 4 |
| 4×3 |
| 2 |
∴展开式中x2项的系数是54.
故答案为:54.
点评:本题考查了二项式定理的应用问题,解题时应弄清二项式系数、展开式中各项的系数是什么,是基础题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
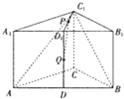 如图,在正三棱柱ABC-A1B1C1中,底面边长为2,侧棱长为
如图,在正三棱柱ABC-A1B1C1中,底面边长为2,侧棱长为