题目内容

已知平面内点M到椭圆
x2
169
+
y2
144
=1的左焦点和右焦点的距离之比为2：3，试求点M的轨迹方程．
考点：圆锥曲线的轨迹问题
专题：计算题,直线与圆,圆锥曲线的定义、性质与方程
分析：求出椭圆
x2
169
+
y2
144
=1的焦点坐标，利用平面内点M到椭圆
x2
169
+
y2
144
=1的左焦点和右焦点的距离之比为2：3，建立方程，化简即可求点M的轨迹方程．
解答： 解：椭圆
x2
169
+
y2
144
=1的焦点坐标为（±5，0），
设M（x，y），则
∵平面内点M到椭圆
x2
169
+
y2
144
=1的左焦点和右焦点的距离之比为2：3，
∴
(x+5)2+y2
(x-5)2+y2
=
2
3
，
化简可得x2+y2+26x+25=0．
点评：本题考查椭圆的性质，考查轨迹方程，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
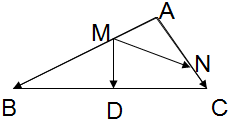如图：在△ABC中，D为BC中点，AM=
1
3
AB，AN=
2
3
AC，设
AB
=
a
，
AC
AC
=
b
．
（Ⅰ）试用
a
，
b
表示
MN
；       
（Ⅱ）试用
a
，
b
表示
MD
．
设函数f（x）是定义在区间（-∞，+∞）上的偶函数，且满足f（1-x）=f（1+x）（x∈R）．
（1）求函数f（x）的周期；
（2）已知当x∈（-1，1]时，f（x）=1-
1-x2
，求使方程f（x）=ax在x∈（-1，1]上有两个不相等实根a的取值集合M；
（3）记Ik=（2k-1，2k+1]（k∈N，k≥1），Mk表示使方程f（x）=ax在x∈Ik上有两个不相等实根的a的取值集合，求集合Mk．
已知函数f（x）=x3+2x2-4x+5．
（1）求曲线y=f（x）在点（1，f（1））处的切线方程；
（2）求函数y=f（x）在[-4，1]上的最大值和最小值．
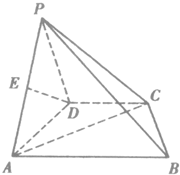如图，在四棱锥P-ABCD中，底面是直角梯形ABCD，其中AD⊥AB，CD∥AB，AB=4，CD=2，侧面PAD与底面ABCD垂直，E为PA的中点．
（1）求证：CD⊥PA；
（2）求证：DE∥平面PBC．
已知集合A={1，b}（b＞1），函数f（x）=
1
2
（x-1）2+1，当x∈A时，f（x）∈A，求b的取值范围．
在集合{（x，y），0≤x≤5，且0≤y≤4}内任取一个元素，能使代数式
y
3
+
x
4
-
19
12
≥0的概率是多少？
先后随机投掷2枚正方体骰子，其中x表示第1枚骰子出现的点数，y表示第2枚骰子出现的点数．
（Ⅰ）求点P（x，y）在直线y=x-1上的概率；
（Ⅱ）求点P（x，y）满足y2＜4x的概率；
（Ⅲ）求在已知x=3的条件下，y≥4的概率．
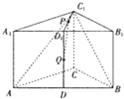如图，在正三棱柱ABC-A1B1C1中，底面边长为2，侧棱长为
2
，D、D1分别为AB、A1B1的中点，C1D1中点为P，DD1中点为Q．
（Ⅰ）求证：PQ∥平面ABC1；
（Ⅱ）求三棱锥Q-ABC1的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网