题目内容
9．下列函数中，是减函数且定义域为（0，+∞）的是（ ）| A． | y=log2x | B． | y=$\frac{1}{x^2}$ | C． | y=$\frac{1}{2^x}$ | D． | y=$\frac{1}{{\sqrt{x}}}$ |
分析 根据常见函数的性质判断对各个选项判断即可．
解答 解：对于A：函数在（0，+∞）递增，不合题意；
对于B：函数的定义域不是（0，+∞），不合题意；
对于C：函数的定义域不是（0，+∞），不合题意；
对于D：函数的定义域是（0，+∞），且在（0，+∞）递减，符合题意；
故选：D．
点评 本题考查了函数的定义域以及函数的单调性问题，是一道基础题．
练习册系列答案
相关题目
19．若不等式x2-2x+a＞0恒成立，则a的取值范围是（ ）
| A． | a＜0 | B． | a＜1 | C． | a＞0 | D． | a＞1 |
20．下列函数中哪个与函数y=x相等（ ）
| A． | y=（$\sqrt{x}$）2 | B． | f（x）=$\frac{{x}^{2}}{x}$ | C． | y=|x| | D． | y=$\root{3}{{x}^{3}}$ |
14．函数f（x）=|${log_{\frac{1}{2}}}$x|的单调递增区间是（ ）
| A． | $（0，\frac{1}{2}]$ | B． | （1，2] | C． | [1，+∞） | D． | （0，+∞） |
1．有下列四个命题，其中假命题是（ ）
| A． | ?x0＞0，x02≤x0 | B． | ?x∈R，3x＞0 | ||
| C． | ?x0∈R，sinx0+cosx0=2 | D． | ?x0∈R，lgx0=0 |
18．
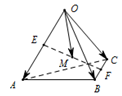如图，E，F分别是四面体OABC的边OA，BC的中点，M为EF的中点，若$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，$\overrightarrow{OC}$=$\overrightarrow{c}$，则下列向量中与$\overrightarrow{OM}$相等的向量是（ ）
如图，E，F分别是四面体OABC的边OA，BC的中点，M为EF的中点，若$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，$\overrightarrow{OC}$=$\overrightarrow{c}$，则下列向量中与$\overrightarrow{OM}$相等的向量是（ ）| A． | -$\frac{1}{4}$$\overrightarrow{a}$-$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$ | B． | $\frac{1}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$ | C． | $\frac{1}{4}$$\overrightarrow{a}$-$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$ | D． | -$\frac{1}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$ |