题目内容
18.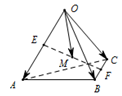 如图,E,F分别是四面体OABC的边OA,BC的中点,M为EF的中点,若$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{OM}$相等的向量是( )
如图,E,F分别是四面体OABC的边OA,BC的中点,M为EF的中点,若$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{OM}$相等的向量是( )| A. | -$\frac{1}{4}$$\overrightarrow{a}$-$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$ | B. | $\frac{1}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$ | C. | $\frac{1}{4}$$\overrightarrow{a}$-$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$ | D. | -$\frac{1}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$ |
分析 利用向量平行四边形法则即可得出.
解答 解:$\overrightarrow{OM}$=$\frac{1}{2}(\overrightarrow{OE}+\overrightarrow{OF})$,$\overrightarrow{OE}=\frac{1}{2}\overrightarrow{a}$,$\overrightarrow{OF}=\frac{1}{2}(\overrightarrow{b}+\overrightarrow{c})$,
∴$\overrightarrow{OM}$=$\frac{1}{4}\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$,
故选:B.
点评 本题考查了向量平行四边形法则,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
9.下列函数中,是减函数且定义域为(0,+∞)的是( )
| A. | y=log2x | B. | y=$\frac{1}{x^2}$ | C. | y=$\frac{1}{2^x}$ | D. | y=$\frac{1}{{\sqrt{x}}}$ |
6.若数列{an}满足:对任意正整数n,{an+1-an}为递减数列,则称数列{an}为“差递减数列”.给出下列数列{an}(n∈N*):
①an=3n,②an=n2+1,③an=$\sqrt{n}$,④an=2n-n,⑤an=ln$\frac{n}{n+1}$
其中是“差递减数列”的有( )
①an=3n,②an=n2+1,③an=$\sqrt{n}$,④an=2n-n,⑤an=ln$\frac{n}{n+1}$
其中是“差递减数列”的有( )
| A. | ③⑤ | B. | ①②④ | C. | ③④⑤ | D. | ②③ |
3.已知双曲线C的中心在坐标原点,F(-2,0)是C的一个焦点,一条渐进线方程为$\sqrt{3}$x-y=0.
(Ⅰ)求双曲线方程;
(Ⅱ)若直线l:y=kx+1与双曲线C有且只有一个公共点,求k的值.
(Ⅰ)求双曲线方程;
(Ⅱ)若直线l:y=kx+1与双曲线C有且只有一个公共点,求k的值.
10.已知抛物线x2=-2y的一条弦AB的中点坐标为(-1,-5),则这条弦AB所在的直线方程是( )
| A. | y=x-4 | B. | y=2x-3 | C. | y=-x-6 | D. | y=3x-2 |
8.设函数f(x)=ex(3x-1)-ax+a,其中a<1,若有且只有一个整数x0使得f(x0)≤0,则a的取值范围是( )
| A. | $(\frac{2}{e},\frac{3}{4})$ | B. | $[\frac{2}{e},\frac{3}{4})$ | C. | $(\frac{2}{e},1)$ | D. | $[\frac{2}{e},1)$ |