题目内容
19.若不等式x2-2x+a>0恒成立,则a的取值范围是( )| A. | a<0 | B. | a<1 | C. | a>0 | D. | a>1 |
分析 根据不等式x2-2x+a>0恒成立时△<0,解不等式即可.
解答 解:不等式x2-2x+a>0恒成立,
则△=4-4a<0,
解得a>1,
所以a的取值范围是a>1.
点评 本题考查了一元二次不等式恒成立的问题,利用判别式即可解答,是基础题目.

练习册系列答案
相关题目
14.已知A,B是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的两个焦点,点C在双曲线上,在△ABC中,sinA:sinB=3:1,则该双曲线的离心率的取值范围为( )
| A. | $(1,\sqrt{3)}$ | B. | $({1,\frac{{\sqrt{10}}}{2}}]$ | C. | (1,2) | D. | (1,2] |
11.若函数f(x)满足关系式f(x)+2f(1-x)=-$\frac{3}{x}$,则f(2)的值为( )
| A. | $-\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | $-\frac{5}{2}$ | D. | $\frac{5}{2}$ |
9.下列函数中,是减函数且定义域为(0,+∞)的是( )
| A. | y=log2x | B. | y=$\frac{1}{x^2}$ | C. | y=$\frac{1}{2^x}$ | D. | y=$\frac{1}{{\sqrt{x}}}$ |
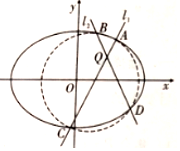 已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>1})$中,a=$\sqrt{2}$b,且椭圆E上任一点到点$P({-\frac{1}{2},0})$的最小距离为$\frac{{\sqrt{7}}}{2}$.
已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>1})$中,a=$\sqrt{2}$b,且椭圆E上任一点到点$P({-\frac{1}{2},0})$的最小距离为$\frac{{\sqrt{7}}}{2}$.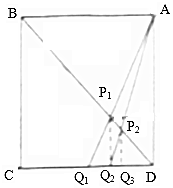 如图,已知ABCD是边长为1的正方形,Q1为CD的中点,Pi(i=1,2…,n)为AQi与BD的交点,过Pi作CD的垂线,垂足为Qi+1,则$\sum_{i=1}^{10}$S${\;}_{△D{Q_i}{P_i}}$=$\frac{5}{24}$.
如图,已知ABCD是边长为1的正方形,Q1为CD的中点,Pi(i=1,2…,n)为AQi与BD的交点,过Pi作CD的垂线,垂足为Qi+1,则$\sum_{i=1}^{10}$S${\;}_{△D{Q_i}{P_i}}$=$\frac{5}{24}$.