题目内容
17.在△ABC中,内角A,B,C所对边的边长分别为a,b,c,已知2sin2$\frac{A}{2}$=$\sqrt{3}$sinA.(I)求角A的大小;
(II)若$\frac{a}{c}$=2cosB,求$\frac{a}{b}$的值.
分析 (I)由已知利用二倍角的正弦函数公式,同角三角函数基本关系式,结合sin$\frac{A}{2}$≠0,可求tan$\frac{A}{2}$=$\sqrt{3}$,由A的范围可求A的值.
(II)由已知利用余弦定理可得b=c,结合A=$\frac{2π}{3}$,利用正弦定理可求$\frac{a}{b}$的值.
解答 (本题满分为14分)
解:(I)∵2sin2$\frac{A}{2}$=$\sqrt{3}$sinA=2$\sqrt{3}$sin$\frac{A}{2}$cos$\frac{A}{2}$,
又0<A<π,可得:0<$\frac{A}{2}$<$\frac{π}{2}$,
故sin$\frac{A}{2}$≠0,
故sin$\frac{A}{2}$=$\sqrt{3}$cos$\frac{A}{2}$,tan$\frac{A}{2}$=$\sqrt{3}$,A=$\frac{2π}{3}$.…7分
(II)由$\frac{a}{c}$=2cosB,得$\frac{a}{c}$=2×$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$,
化简得b=c,…10分
故在△ABC中,A=$\frac{2π}{3}$,b=c,
由此可得$\frac{a}{b}$=$\frac{sinA}{sinB}$=$\sqrt{3}$.…14分.
点评 本题主要考查了二倍角的正弦函数公式,同角三角函数基本关系式,余弦定理,正弦定理在解三角形中的应用,考查了计算能力和转化思想,属于中档题.

练习册系列答案
相关题目
5.在某次物理实验中,得到一组不全相等的数据x1,x2,x3,…,xn,若a是这组数据的算术平均数,则a满足( )
| A. | $\sum_{i=1}^{n}$(xi-a)最小 | B. | $\sum_{i=1}^{n}$|xi-a|最小 | ||
| C. | $\sum_{i=1}^{n}$(xi-a)2最小 | D. | $\frac{1}{n}$$\sum_{i=1}^{n}$|xi-a|最小 |
2.函数f(x)=log2$\frac{x}{2}$•log2$\frac{x}{4}$,x∈(2,8]的值域为( )
| A. | [0,2] | B. | [-$\frac{1}{4}$,2] | C. | (0,2] | D. | (-$\frac{1}{4}$,2] |
9.下列函数中,是减函数且定义域为(0,+∞)的是( )
| A. | y=log2x | B. | y=$\frac{1}{x^2}$ | C. | y=$\frac{1}{2^x}$ | D. | y=$\frac{1}{{\sqrt{x}}}$ |
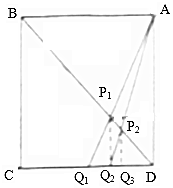 如图,已知ABCD是边长为1的正方形,Q1为CD的中点,Pi(i=1,2…,n)为AQi与BD的交点,过Pi作CD的垂线,垂足为Qi+1,则$\sum_{i=1}^{10}$S${\;}_{△D{Q_i}{P_i}}$=$\frac{5}{24}$.
如图,已知ABCD是边长为1的正方形,Q1为CD的中点,Pi(i=1,2…,n)为AQi与BD的交点,过Pi作CD的垂线,垂足为Qi+1,则$\sum_{i=1}^{10}$S${\;}_{△D{Q_i}{P_i}}$=$\frac{5}{24}$.