题目内容
将一枚骰子先后抛掷2次,观察向上的点数,求:
(1)两数之和为6的概率;
(2)两数之和是3的倍数的概率;
(3)两数之积是6的倍数的概率;
(4)以第一次向上的点数为横坐标x、第二次向上的点数为纵坐标y的点(x,y)在圆x2+y2=25的内部的概率.
(1)两数之和为6的概率;
(2)两数之和是3的倍数的概率;
(3)两数之积是6的倍数的概率;
(4)以第一次向上的点数为横坐标x、第二次向上的点数为纵坐标y的点(x,y)在圆x2+y2=25的内部的概率.
考点:列举法计算基本事件数及事件发生的概率
专题:应用题,概率与统计
分析:(1)由题意知本题是一个等可能事件的概率,试验发生包含的事件数是6×6种结果,满足条件是事件是两个数字的和是6的可以列举出共有5种结果,得到概率.
(2)记两数之和是3的倍数为事件A,由基本事件的列表易得事件A中含有的基本事件数目,由古典概型公式可得答案;
(3)记“向上的两数之积是6的倍数”为事件B,由基本事件的列表易得事件A中含有的基本事件数目,由古典概型公式可得答案;
(4)由题意知本题是一个等可能事件的概率,试验发生包含的事件数是6×6种结果,列举出符合条件的事件数,得到概率.
(2)记两数之和是3的倍数为事件A,由基本事件的列表易得事件A中含有的基本事件数目,由古典概型公式可得答案;
(3)记“向上的两数之积是6的倍数”为事件B,由基本事件的列表易得事件A中含有的基本事件数目,由古典概型公式可得答案;
(4)由题意知本题是一个等可能事件的概率,试验发生包含的事件数是6×6种结果,列举出符合条件的事件数,得到概率.
解答:
解:(1)由题意知本题是一个等可能事件的概率,
试验发生包含的事件数是6×6=36种结果,
满足条件是事件是两个数字的和是6,共有(1,5)(2,4)(3,3)(4,2)(5,1)五种情况,
∴两数之和为6的概率是
.
(2)记“两数之和是3的倍数”为事件B,则事件B中含有
(1,2),(1,5),(2,1),(2,4),(3,3),(3,6),(4,2),(4,5),(5,1),(5,4),(6,3),(6,6)共12个基本事件,
故两数之和是3的倍数的概率为:P(B)=
=
(3)记“向上的两数之积是6的倍数”为事件B,则由列表可知,事件B中含有其中的15个等可能基本事件,
所以P(B)=
=
;
(4)由题意知本题是一个等可能事件的概率,
试验发生包含的事件数是6×6=36种结果,
第一次向上点数为横坐标x,第二次向上的点数为纵坐标y的点(x,y)
当x=1时,y有1,2,3,4,4种结果,
当x=2时,y有1,2,3,4,4种结果,
当x=3时,y有1,2,3,3种结果,
当x=4时,y有1,2,2种结果,
∴共有4+4+3+2=13种结果.
∴要求的概率是
试验发生包含的事件数是6×6=36种结果,
满足条件是事件是两个数字的和是6,共有(1,5)(2,4)(3,3)(4,2)(5,1)五种情况,
∴两数之和为6的概率是
| 5 |
| 36 |
(2)记“两数之和是3的倍数”为事件B,则事件B中含有
(1,2),(1,5),(2,1),(2,4),(3,3),(3,6),(4,2),(4,5),(5,1),(5,4),(6,3),(6,6)共12个基本事件,
故两数之和是3的倍数的概率为:P(B)=
| 12 |
| 36 |
| 1 |
| 3 |
(3)记“向上的两数之积是6的倍数”为事件B,则由列表可知,事件B中含有其中的15个等可能基本事件,
所以P(B)=
| 15 |
| 36 |
| 5 |
| 12 |
(4)由题意知本题是一个等可能事件的概率,
试验发生包含的事件数是6×6=36种结果,
第一次向上点数为横坐标x,第二次向上的点数为纵坐标y的点(x,y)
当x=1时,y有1,2,3,4,4种结果,
当x=2时,y有1,2,3,4,4种结果,
当x=3时,y有1,2,3,3种结果,
当x=4时,y有1,2,2种结果,
∴共有4+4+3+2=13种结果.
∴要求的概率是
| 13 |
| 36 |
点评:本题考查等可能事件的概率,注意解题过程中利用的列举的方法,做出事件数,本题是一个概率知识点的基础题.

练习册系列答案
相关题目
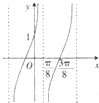 已知函数f(x)=Atan(ωx+φ)(ω>0,|φ|<
已知函数f(x)=Atan(ωx+φ)(ω>0,|φ|<| π |
| 2 |
| 3 |
A、
| ||||
B、
| ||||
C、kπ+
| ||||
D、
|
二面角α-l-β中,平面α的一个法向量n1=(
,-
,-
),平面β的一个法向量n2=(0,
,
],则二面角α-l-β的大小为( )
| ||
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| A、120° |
| B、150° |
| C、30°或150° |
| D、60°或120° |