题目内容
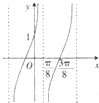已知函数f（x）=Atan（ωx+φ）（ω＞0，|φ|＜| π |
| 2 |
| 3 |
A、
| ||||
B、
| ||||
C、kπ+
| ||||
D、
|
考点：正切函数的图象
专题：三角函数的图像与性质
分析：根据三角函数的图象和性质即可得到结论．
解答：
解：由图象可知函数的周期T=2（
-
）=2×
=
，
则T=
=
，解得ω=2，
当
时，函数值为0，则2×
+φ=kπ，
解得φ=kπ-
，
∵|φ|＜
，∴当k=0时，φ=
，
即f（x）=Atan（2x+
），
∵f（0）=1，∴Atan
=1，即A=1，
则f（x）=tan（2x+
），
由f（x0）=tan（2x0+
）=
，
即2x0+
=kπ+
，
则
+
，k∈Z，
故选：B
| 3π |
| 8 |
| π |
| 8 |
| 2π |
| 8 |
| π |
| 2 |
则T=
| π |
| ω |
| π |
| 2 |
当
| 3π |
| 8 |
| 3π |
| 8 |
解得φ=kπ-
| 3π |
| 4 |
∵|φ|＜
| π |
| 2 |
| π |
| 4 |
即f（x）=Atan（2x+
| π |
| 4 |
∵f（0）=1，∴Atan
| π |
| 4 |
则f（x）=tan（2x+
| π |
| 4 |
由f（x0）=tan（2x0+
| π |
| 4 |
| 3 |
即2x0+
| π |
| 4 |
| π |
| 3 |
则
| kπ |
| 2 |
| π |
| 24 |
故选：B
点评：本题主要考查正切函数的图象和性质，根据图象确定函数的周期是解决本题的关键．
练习册系列答案
相关题目
设集合A={x|x2-1＜0}，B={x|y=
}，则A∩B等于（ ）
log
|
| A、{x|x＞1} |
| B、{x|0＜x＜1} |
| C、{x|x＜1} |
| D、{x|0＜x≤1} |
直三棱柱ABC-A′B′C′各侧棱和底面边长均为a，点D是CC′上任意一点，连结A′B，BD，A′D，AD，则三棱锥A-A′BD的体积（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
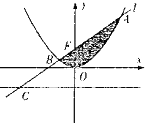如图，过抛物线x2=2py（p＞0）的焦点F的直线l交抛物线于A，B两点，交其准线于点C，若|BC|=