题目内容
设a,b∈R,则“(a-b)a2>0”是“a>b”的( )
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、非充分非必要条件 |
| D、充要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据不等式的性质,利用充分条件和必要条件的定义进行判断.
解答:
解:若(a-b)a2>0,则a≠0且a-b>0,即a>b成立.
当a=0,b=-1时,满足a>b,但(a-b)a2>0不成立,
∴“(a-b)a2>0”是“a>b”的充分不必要条件.
故选:A.
当a=0,b=-1时,满足a>b,但(a-b)a2>0不成立,
∴“(a-b)a2>0”是“a>b”的充分不必要条件.
故选:A.
点评:本题主要考查充分条件和必要条件的判断,利用不等式的性质是解决本题的关键.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案
相关题目
下列说法中正确的是( )
| A、若命题p为:对?x∈R有x2>0,则¬p:?x∈R使x2≤0 | ||||
B、若命题p为:
| ||||
| C、若p是q的充分不必要条件,则¬p是¬q的必要不充分条件 | ||||
D、方程ax2+x+a=0有唯一解的充要条件是:a=±
|
已知双曲线标准方程为
-x2=1,则双曲线离心率为( )
| y2 |
| 2 |
A、
| ||||
| B、3 | ||||
C、
| ||||
D、
|
某商品销售量y(件)与销售价格x(元/件)负相关,则其回归方程可能是( )
A、
| ||
B、
| ||
C、
| ||
D、
|

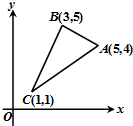 如图,已知可行域为△ABC及其内部,若目标函数z=kx+y当且仅当在点B处取得最大值,则k的取值范围是
如图,已知可行域为△ABC及其内部,若目标函数z=kx+y当且仅当在点B处取得最大值,则k的取值范围是