题目内容
设α、β是两个不重合的平面,m、n是两条不重合的直线,则以下结论错误的是( )
| A、若α∥β,m?α,则 m∥β |
| B、若m∥α,m∥β,α∩β=n,则 m∥n |
| C、若m?α,n?α,m∥β,n∥β,则α∥β |
| D、若m∥α,m⊥β,则α⊥β |
考点:空间中直线与平面之间的位置关系
专题:综合题,空间位置关系与距离
分析:若α∥β,m?α,根据面面平行的性质,可得m∥β;
若m∥α,m∥β,α∩β=n,根据线面平行的性质,可得m∥n;
若“m?α,n?α,m∥β,n∥β,且m∩n=O”,则“α∥β”成立,但条件中缺少了“m∩n=O”,故结论“α∥β”不一定成立;
若m∥α,经过m的平面与α相交于a,则可得m中m∥a,由于m⊥β,所以a⊥β,根据面面垂直的判定定理,可得α⊥β.
若m∥α,m∥β,α∩β=n,根据线面平行的性质,可得m∥n;
若“m?α,n?α,m∥β,n∥β,且m∩n=O”,则“α∥β”成立,但条件中缺少了“m∩n=O”,故结论“α∥β”不一定成立;
若m∥α,经过m的平面与α相交于a,则可得m中m∥a,由于m⊥β,所以a⊥β,根据面面垂直的判定定理,可得α⊥β.
解答:
解:若α∥β,m?α,根据面面平行的性质,可得m∥β,故A正确;
若m∥α,m∥β,α∩β=n,根据线面平行的性质,可得m∥n,故B正确;
若“m?α,n?α,m∥β,n∥β,且m∩n=O”,则“α∥β”成立,但条件中缺少了“m∩n=O”,故结论“α∥β”不一定成立,得C错误;
若m∥α,经过m的平面与α相交于a,则可得m中m∥a,由于m⊥β,所以a⊥β,根据面面垂直的判定定理,可得α⊥β,故D正确.
故选:C.
若m∥α,m∥β,α∩β=n,根据线面平行的性质,可得m∥n,故B正确;
若“m?α,n?α,m∥β,n∥β,且m∩n=O”,则“α∥β”成立,但条件中缺少了“m∩n=O”,故结论“α∥β”不一定成立,得C错误;
若m∥α,经过m的平面与α相交于a,则可得m中m∥a,由于m⊥β,所以a⊥β,根据面面垂直的判定定理,可得α⊥β,故D正确.
故选:C.
点评:本题给出空间位置关系的几个命题,判断其真假,着重考查了线面平行的定义与性质、面面平行的判定定理和面面垂直的性质等知识,属于基础题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
已知双曲线标准方程为
-x2=1,则双曲线离心率为( )
| y2 |
| 2 |
A、
| ||||
| B、3 | ||||
C、
| ||||
D、
|
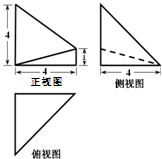 已知某几何体的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形,则此几何体的体积V为( )
已知某几何体的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形,则此几何体的体积V为( )A、
| ||
B、
| ||
C、
| ||
| D、40 |
某商品销售量y(件)与销售价格x(元/件)负相关,则其回归方程可能是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
