题目内容
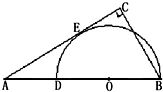如图，BD是半圆O的直径，A在BD的延长线上，AC与半圆相切于点E，AC⊥BC，若AD=2| 3 |
考点：与圆有关的比例线段
专题：计算题
分析：连结OE，由切线的性质定理得到OE⊥AC，从而可得OE∥BC．根据切割线定理得AE2=AD•AB，解出AB=6
，可得AO=4
，最后利用比例线段加以计算得到AC长，从而可得EC的长．
| 3 |
| 3 |
解答：
解：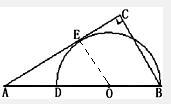
连结OE，
∵AC与半圆相切于点E，∴OE⊥AC，
又∵AC⊥BC，∴OE∥BC．
由切割线定理，得AE2=AD•AB，即36=2
•AB，解得AB=6
，
因此，半圆的直径BD=4
，AO=BD=4
．
可得
=
=
，所以AC=
AE=9，EC=AC-AE=3．
故答案为：3
连结OE，∵AC与半圆相切于点E，∴OE⊥AC，
又∵AC⊥BC，∴OE∥BC．
由切割线定理，得AE2=AD•AB，即36=2
| 3 |
| 3 |
因此，半圆的直径BD=4
| 3 |
| 3 |
可得
| AE |
| AC |
| AO |
| AB |
| 2 |
| 3 |
| 3 |
| 2 |
故答案为：3
点评：本题给出半圆满足的条件，求线段EC之长．着重考查了切线的性质定理、切割线定理与相似三角形等知识，属于中档题．
练习册系列答案
互动课堂系列答案
激活思维智能训练课时导学练系列答案
相关题目
过抛物线y2=4x的焦点作一条直线与抛物线相交于A、B两点，它们的横坐标之和等于2，则这样的直线（ ）
| A、有且仅有一条 |
| B、有且仅有两条 |
| C、有无穷多条 |
| D、不存在 |
已知角θ满足
＞0，且cosθ•tanθ＜0，则角θ的终边在（ ）
| sinθ |
| tanθ |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
函数f（x）=
•
，奇偶性判断正确的是（ ）
| x2-1 |
| 1-x2 |
| A、是偶函数但不是奇函数 |
| B、既是奇函数又是偶函数 |
| C、是奇函数但不是偶函数 |
| D、既不是奇函数又不是偶函数 |