题目内容
设常数a>0,若9x+
≥a+1对一切正实数x成立,则a的取值范围为 .
| a2 |
| x |
考点:基本不等式
专题:不等式的解法及应用
分析:9x+
≥a+1对一切正实数x成立?a+1≤(9x+
)min.再利用基本不等式即可得出.
| a2 |
| x |
| a2 |
| x |
解答:
解:∵x>0,a>0,∴9x+
≥2
=6a,当且仅当x=
时取等号.
∵9x+
≥a+1对一切正实数x成立,∴a+1≤(9x+
)min.
∴a+1≤6a,解得a≥
.
∴a的取值范围为[
,+∞).
故答案为:[
,+∞).
| a2 |
| x |
9x•
|
| a |
| 3 |
∵9x+
| a2 |
| x |
| a2 |
| x |
∴a+1≤6a,解得a≥
| 1 |
| 5 |
∴a的取值范围为[
| 1 |
| 5 |
故答案为:[
| 1 |
| 5 |
点评:本题考查了基本不等式的性质、恒成立问题的等价转化,属于基础题.

练习册系列答案
 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
(2x3+
)7的展开式中常数项是( )
| 1 | ||
|
| A、14 | B、-14 |
| C、42 | D、-42 |
在椭圆
+
=1内,通过点M(1,1),且被这点平分的弦所在的直线方程为( )
| x2 |
| 16 |
| y2 |
| 4 |
| A、x+4y-5=0 |
| B、x-4y-5=0 |
| C、4x+y-5=0 |
| D、4x-y-5=0 |
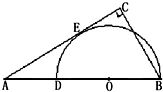 如图,BD是半圆O的直径,A在BD的延长线上,AC与半圆相切于点E,AC⊥BC,若
如图,BD是半圆O的直径,A在BD的延长线上,AC与半圆相切于点E,AC⊥BC,若