题目内容
已知一动圆与圆O1:(x+2)2+y2=49内切,与圆O2:(x-2)2+y2=1的外切,求动圆圆心P的轨迹方程.
考点:轨迹方程
专题:综合题,直线与圆,圆锥曲线的定义、性质与方程
分析:由动圆与圆O1内切,与圆O2的外切,可得|PO1|=7-r,|PO2|=1+r,|O1O2|=4,故有|PO1|+|PO2|=8>|O1O2|,利用椭圆定义,可求动圆圆心P的轨迹方程.
解答:
解:设点P坐标为(x,y),动圆半径为r.
由圆O1:(x+2)2+y2=49,圆O2:(x-2)2+y2=1
可知O1(-2,0),O2(2,0),r1=7,r2=1…(4分)
因为动圆与圆O1内切,与圆O2的外切,
所以|PO1|=7-r,|PO2|=1+r,|O1O2|=4…(7分)
故有|PO1|+|PO2|=8>|O1O2|…(10分)
由椭圆定义可知,动圆圆心P的轨迹是以O1,O2为焦点,长轴长为8的椭圆,…(12分)
方程为:
+
=1…(14分)
由圆O1:(x+2)2+y2=49,圆O2:(x-2)2+y2=1
可知O1(-2,0),O2(2,0),r1=7,r2=1…(4分)
因为动圆与圆O1内切,与圆O2的外切,
所以|PO1|=7-r,|PO2|=1+r,|O1O2|=4…(7分)
故有|PO1|+|PO2|=8>|O1O2|…(10分)
由椭圆定义可知,动圆圆心P的轨迹是以O1,O2为焦点,长轴长为8的椭圆,…(12分)
方程为:
| x2 |
| 16 |
| y2 |
| 12 |
点评:本题考查轨迹方程,考查圆与圆的位置关系,考查椭圆的定义,正确理解椭圆的定义是关键.

练习册系列答案
相关题目
点M(3,-4)和点N(m,n)关于直线y=x对称,则( )
| A、m=-4,n=-3 |
| B、m=4,n=-3 |
| C、m=-4,n=3 |
| D、m=4,n=3 |
把189化为三进制数,则末位数是( )
| A、0 | B、1 | C、2 | D、3 |
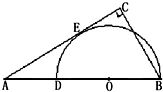 如图,BD是半圆O的直径,A在BD的延长线上,AC与半圆相切于点E,AC⊥BC,若
如图,BD是半圆O的直径,A在BD的延长线上,AC与半圆相切于点E,AC⊥BC,若