题目内容
多选题是标准化考试的一种题型,一般是从A、B、C、D四个选项中选出所有正确的答案.在一次考试中有5道多选题,某同学一道都不会,他随机的猜测,则他答对题数的期望值为 .
考点:离散型随机变量的期望与方差
专题:概率与统计
分析:由已知条件,先求出该同学答对每道题的概率p,再设该同学在5道多选题中答对的题数为ξ,则ξ~B(5,p),由此能求出结果.
解答:
解:由题意知,该同事答对每道题的概率都是:
p=
=
,
设该同学在5道多选题中答对的题数为ξ,
则ξ~B(5,
),
∴该同学答对题数的期望值Eξ=5×
=
.
故答案为:
.
p=
| 1 | ||||||||
|
| 1 |
| 5 |
设该同学在5道多选题中答对的题数为ξ,
则ξ~B(5,
| 1 |
| 15 |
∴该同学答对题数的期望值Eξ=5×
| 1 |
| 15 |
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:本题考查离散型随机变量的数学期望的求法,是中档题,解题时要认真审题,注意概率知识的合理运用.

练习册系列答案
相关题目
点M(3,-4)和点N(m,n)关于直线y=x对称,则( )
| A、m=-4,n=-3 |
| B、m=4,n=-3 |
| C、m=-4,n=3 |
| D、m=4,n=3 |
 选修4-1:几何证明选讲
选修4-1:几何证明选讲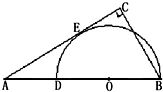 如图,BD是半圆O的直径,A在BD的延长线上,AC与半圆相切于点E,AC⊥BC,若
如图,BD是半圆O的直径,A在BD的延长线上,AC与半圆相切于点E,AC⊥BC,若