题目内容
过抛物线y2=4x的焦点作一条直线与抛物线相交于A、B两点,它们的横坐标之和等于2,则这样的直线( )
| A、有且仅有一条 |
| B、有且仅有两条 |
| C、有无穷多条 |
| D、不存在 |
考点:直线与圆锥曲线的关系
专题:综合题,圆锥曲线的定义、性质与方程
分析:过抛物线y2=4x的焦点作一条直线与抛物线相交于A、B两点,先看直线AB斜率不存在时,求得横坐标之和等于2,符合题意;进而设直线AB为y=k(x-1)与抛物线方程联立消去y,进而根据韦达定理表示出A、B两点的横坐标之和,方程无解,进而得出结论.
解答:
解:过抛物线y2=4x的焦点作一条直线与抛物线相交于A、B两点,
若直线AB的斜率不存在,则横坐标之和等于2,适合.
故设直线AB的斜率为k,则直线AB方程为y=k(x-1)
代入抛物线y2=4x得,k2x2-2(k2+2)x+k2=0
∵A、B两点的横坐标之和等于2,
∴
=2,
∴方程无解,
∴这样的直线不存在.
故选A.
若直线AB的斜率不存在,则横坐标之和等于2,适合.
故设直线AB的斜率为k,则直线AB方程为y=k(x-1)
代入抛物线y2=4x得,k2x2-2(k2+2)x+k2=0
∵A、B两点的横坐标之和等于2,
∴
| 2(k2+2) |
| k2 |
∴方程无解,
∴这样的直线不存在.
故选A.
点评:本题主要考查了直线与抛物线的位置关系,考查分类讨论的数学思想,考查学生的计算能力,属于中档题.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案
相关题目
已知等差数列的前n项和为18,若S3=1,an+an-1+an-2=3,则n的值为( )
| A、9 | B、21 | C、27 | D、36 |
已知圆C:x2+y2-2ax-4y+a2=0 (a>O)及直线l:x-y+3=0,当直线l被圆C截得的弦长为2
时,a=( )
| 3 |
A、
| ||
B、2-
| ||
C、
| ||
D、
|
在△ABC中,角A,B,C所对的边分别为a,b,c,若acosA=bsinB,则
sin2A+cos2B=( )
| 1 |
| 2 |
A、
| ||
B、-
| ||
| C、-1 | ||
| D、1 |
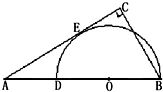 如图,BD是半圆O的直径,A在BD的延长线上,AC与半圆相切于点E,AC⊥BC,若
如图,BD是半圆O的直径,A在BD的延长线上,AC与半圆相切于点E,AC⊥BC,若