题目内容
函数f(x)=
•
,奇偶性判断正确的是( )
| x2-1 |
| 1-x2 |
| A、是偶函数但不是奇函数 |
| B、既是奇函数又是偶函数 |
| C、是奇函数但不是偶函数 |
| D、既不是奇函数又不是偶函数 |
考点:函数奇偶性的判断
专题:函数的性质及应用
分析:先求出函数的定义域,然后根据函数奇偶性的定义进行判断即可.
解答:
解:要使函数有意义,则
,
即
,
∴x2=1,即x=±1,
即函数的定义域为{1,-1},
∵f(1)=f(-1)=0,
∴f(x)既是奇函数又是偶函数,
故选:B.
|
即
|
∴x2=1,即x=±1,
即函数的定义域为{1,-1},
∵f(1)=f(-1)=0,
∴f(x)既是奇函数又是偶函数,
故选:B.
点评:本题主要考查函数奇偶性的判断,判断函数的奇偶性要先判断函数的定义域是否关于原点对称.

练习册系列答案
相关题目
已知圆C:x2+y2-2ax-4y+a2=0 (a>O)及直线l:x-y+3=0,当直线l被圆C截得的弦长为2
时,a=( )
| 3 |
A、
| ||
B、2-
| ||
C、
| ||
D、
|
在椭圆
+
=1内,通过点M(1,1),且被这点平分的弦所在的直线方程为( )
| x2 |
| 16 |
| y2 |
| 4 |
| A、x+4y-5=0 |
| B、x-4y-5=0 |
| C、4x+y-5=0 |
| D、4x-y-5=0 |
在△ABC中,角A,B,C所对的边分别为a,b,c,若acosA=bsinB,则
sin2A+cos2B=( )
| 1 |
| 2 |
A、
| ||
B、-
| ||
| C、-1 | ||
| D、1 |
点M(3,-4)和点N(m,n)关于直线y=x对称,则( )
| A、m=-4,n=-3 |
| B、m=4,n=-3 |
| C、m=-4,n=3 |
| D、m=4,n=3 |
把189化为三进制数,则末位数是( )
| A、0 | B、1 | C、2 | D、3 |
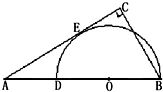 如图,BD是半圆O的直径,A在BD的延长线上,AC与半圆相切于点E,AC⊥BC,若
如图,BD是半圆O的直径,A在BD的延长线上,AC与半圆相切于点E,AC⊥BC,若