题目内容
已知角θ满足
>0,且cosθ•tanθ<0,则角θ的终边在( )
| sinθ |
| tanθ |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
考点:三角函数值的符号
专题:三角函数的图像与性质
分析:由
,可得θ为第一或四象限角,由cosθ•tanθ<0,可得θ为第三或四象限角,综合可得.
| sinθ |
| tanθ |
解答:
解:∵
>0,即sinθ与tanθ同号,
∴θ为第一或四象限角,
又cosθ•tanθ<0,即cosθ与tanθ异号,
∴θ为第三或四象限角,
综上可得θ为第四象限角,
故选:D.
| sinθ |
| tanθ |
∴θ为第一或四象限角,
又cosθ•tanθ<0,即cosθ与tanθ异号,
∴θ为第三或四象限角,
综上可得θ为第四象限角,
故选:D.
点评:本题考查三角函数的符号与角的象限的关系,属基础题.

练习册系列答案
相关题目
(2x3+
)7的展开式中常数项是( )
| 1 | ||
|
| A、14 | B、-14 |
| C、42 | D、-42 |
已知圆C:x2+y2-2ax-4y+a2=0 (a>O)及直线l:x-y+3=0,当直线l被圆C截得的弦长为2
时,a=( )
| 3 |
A、
| ||
B、2-
| ||
C、
| ||
D、
|
在椭圆
+
=1内,通过点M(1,1),且被这点平分的弦所在的直线方程为( )
| x2 |
| 16 |
| y2 |
| 4 |
| A、x+4y-5=0 |
| B、x-4y-5=0 |
| C、4x+y-5=0 |
| D、4x-y-5=0 |
点M(3,-4)和点N(m,n)关于直线y=x对称,则( )
| A、m=-4,n=-3 |
| B、m=4,n=-3 |
| C、m=-4,n=3 |
| D、m=4,n=3 |
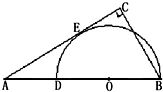 如图,BD是半圆O的直径,A在BD的延长线上,AC与半圆相切于点E,AC⊥BC,若
如图,BD是半圆O的直径,A在BD的延长线上,AC与半圆相切于点E,AC⊥BC,若