题目内容
5.函数y=logax(a>0且a≠1)的图象经过点$(\;2\sqrt{2}\;,\;-1\;)$,函数y=bx(b>0且b≠1)的图象经过点$(\;1\;,\;2\sqrt{2})$,则下列关系式中正确的是( )| A. | a2>b2 | B. | 2a>2b | C. | ${({\frac{1}{2}})^a}>{({\frac{1}{2}})^b}$ | D. | (a${\;}^{\frac{1}{2}}$>b${\;}^{\frac{1}{2}}$) |
分析 由已知条件,把点的坐标代入对应的函数解析式,求出a=$\frac{\sqrt{2}}{4}$、b=2$\sqrt{2}$,从而可得结论.
解答 解:∵函数y=logax(a>0且a≠1)的图象经过点$(\;2\sqrt{2}\;,\;-1\;)$,
∴loga 2$\sqrt{2}$=-1,
∴a=$\frac{\sqrt{2}}{4}$.
由于函数y=bx(b>0且b≠1)的图象经过点(1,2$\sqrt{2}$),故有b1=2$\sqrt{2}$,即 b=2$\sqrt{2}$.
故有 b>a>0,
∴${({\frac{1}{2}})^a}>{({\frac{1}{2}})^b}$,
故选:C.
点评 本题主要考查对数函数的单调性和特殊点,指数函数的单调性和特殊点,求出a=$\frac{\sqrt{2}}{4}$、b=2$\sqrt{2}$是解题的关键,属于中档题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
16.“a=0”是“直线l1:ax+y-1=0与直线l2:x+ay-1=0垂直”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
20.一架战斗机以1000$\sqrt{2}$千米/小时速度朝东偏北45°方向水平飞行,发现正东100千米外同高度有一架民航飞机正在以800千米/小时速度朝正北飞行,如双方都不改变速度与航向,两机最小距离在哪个区间内(单位:千米)( )
| A. | (0,5) | B. | (5,10) | C. | (10,15) | D. | (15,20) |
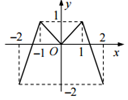 如图,定义在[-2,2]的偶函数f(x)的图象如图所示,函数g(x)=f(x)-$\frac{1}{4}x+\frac{1}{2}$的零点个数为( )
如图,定义在[-2,2]的偶函数f(x)的图象如图所示,函数g(x)=f(x)-$\frac{1}{4}x+\frac{1}{2}$的零点个数为( )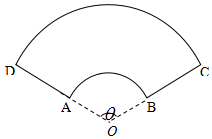 某公司拟设计一个扇环形状的花坛(如图所示),该扇环是由以点O为圆心的两个同心圆弧和延长后通过点AD的两条线段围成.设圆弧$\widehat{AB}$、$\widehat{CD}$所在圆的半径分别为f(x)、R米,圆心角为θ(弧度).
某公司拟设计一个扇环形状的花坛(如图所示),该扇环是由以点O为圆心的两个同心圆弧和延长后通过点AD的两条线段围成.设圆弧$\widehat{AB}$、$\widehat{CD}$所在圆的半径分别为f(x)、R米,圆心角为θ(弧度).