题目内容
15.双曲线C:x2-4y2=1的渐近线方程是y=±$\frac{1}{2}$x,双曲线C的离心率是$\frac{\sqrt{5}}{2}$.分析 将双曲线的方程化为标准方程,求得a,b,c,即可得到所求渐近线方程和离心率.
解答 解:双曲线C:x2-4y2=1,
即为$\frac{{x}^{2}}{1}$-$\frac{{y}^{2}}{\frac{1}{4}}$=1,
可得a=1,b=$\frac{1}{2}$,c=$\sqrt{{a}^{2}+{b}^{2}}$=$\frac{\sqrt{5}}{2}$,
可得渐近线方程为y=±$\frac{1}{2}$x;
离心率e=$\frac{c}{a}$=$\frac{\sqrt{5}}{2}$.
故答案为:y=±$\frac{1}{2}$x;$\frac{\sqrt{5}}{2}$.
点评 本题考查双曲线的方程和性质,主要是渐近线方程和离心率的求法,属于基础题.

练习册系列答案
相关题目
3.$cos\frac{2017π}{3}$等于( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
4.设F1,F2分别为双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1(a>0,b>0)$的两个焦点,M,N是双曲线C的一条渐近线上的两点,四边形MF1NF2为矩形,A为双曲线的一个顶点,若△AMN的面积为$\frac{1}{2}{c}^{2}$,则该双曲线的离心率为( )
| A. | 3 | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
5.函数y=logax(a>0且a≠1)的图象经过点$(\;2\sqrt{2}\;,\;-1\;)$,函数y=bx(b>0且b≠1)的图象经过点$(\;1\;,\;2\sqrt{2})$,则下列关系式中正确的是( )
| A. | a2>b2 | B. | 2a>2b | C. | ${({\frac{1}{2}})^a}>{({\frac{1}{2}})^b}$ | D. | (a${\;}^{\frac{1}{2}}$>b${\;}^{\frac{1}{2}}$) |
 如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC⊥CB,点M和N分别是B1C1和BC的中点.
如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC⊥CB,点M和N分别是B1C1和BC的中点.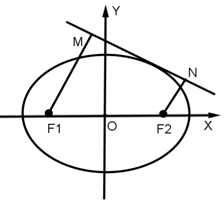 已知椭圆C的方程是$\frac{x^2}{4}+\frac{y^2}{3}=1$,直线l:y=kx+m与椭圆C有且仅有一个公共点,若F1M⊥l,F2N⊥l,M,N分别为垂足.
已知椭圆C的方程是$\frac{x^2}{4}+\frac{y^2}{3}=1$,直线l:y=kx+m与椭圆C有且仅有一个公共点,若F1M⊥l,F2N⊥l,M,N分别为垂足.