题目内容
10.二项式($\sqrt{3}$x+$\root{3}{2}$)n(n∈N*)展开式中只有一项的系数为有理数,则n可能取值为( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
分析 由题意,展开式中项的系数为${C}_{n}^{r}•{3}^{\frac{n-r}{2}}•{2}^{\frac{r}{3}}$,系数为有理数,n-r是2的倍数,r是3的倍数,代入验证,即可得出结论.
解答 解:由题意,展开式中项的系数为${C}_{n}^{r}•{3}^{\frac{n-r}{2}}•{2}^{\frac{r}{3}}$,
系数为有理数,n-r是2的倍数,r是3的倍数,
n=6,r=0,6不符合;n=7,r=3;n=8,r=0,6不符合;n=9,r=3,9,不符合题意,
故选B.
点评 本题考查二项展开式,考查学生的计算能力,属于中档题.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
1.如图是函数f(x)=cos(πx+φ)(0<φ<$\frac{π}{2}$)的部分图象,则f(3x0)=( )


| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
5.函数y=logax(a>0且a≠1)的图象经过点$(\;2\sqrt{2}\;,\;-1\;)$,函数y=bx(b>0且b≠1)的图象经过点$(\;1\;,\;2\sqrt{2})$,则下列关系式中正确的是( )
| A. | a2>b2 | B. | 2a>2b | C. | ${({\frac{1}{2}})^a}>{({\frac{1}{2}})^b}$ | D. | (a${\;}^{\frac{1}{2}}$>b${\;}^{\frac{1}{2}}$) |
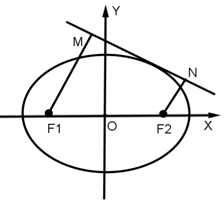 已知椭圆C的方程是$\frac{x^2}{4}+\frac{y^2}{3}=1$,直线l:y=kx+m与椭圆C有且仅有一个公共点,若F1M⊥l,F2N⊥l,M,N分别为垂足.
已知椭圆C的方程是$\frac{x^2}{4}+\frac{y^2}{3}=1$,直线l:y=kx+m与椭圆C有且仅有一个公共点,若F1M⊥l,F2N⊥l,M,N分别为垂足. 如图,在平行六面体ABCD-A1B1C1D1中,底面是边长为2的正方形,若$∠{A_1}AB=∠{A_1}AD={60^0}$,且A1A=3,则A1C的长为$\sqrt{17}$.
如图,在平行六面体ABCD-A1B1C1D1中,底面是边长为2的正方形,若$∠{A_1}AB=∠{A_1}AD={60^0}$,且A1A=3,则A1C的长为$\sqrt{17}$.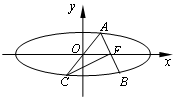 如图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右焦点为F,过F的直线交椭圆于A,B两点,点C是点A关于原点O的对称点,若CF⊥AB且CF=AB,则椭圆的离心率为$\sqrt{6}-\sqrt{3}$.
如图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右焦点为F,过F的直线交椭圆于A,B两点,点C是点A关于原点O的对称点,若CF⊥AB且CF=AB,则椭圆的离心率为$\sqrt{6}-\sqrt{3}$.