题目内容
20．一架战斗机以1000$\sqrt{2}$千米/小时速度朝东偏北45°方向水平飞行，发现正东100千米外同高度有一架民航飞机正在以800千米/小时速度朝正北飞行，如双方都不改变速度与航向，两机最小距离在哪个区间内（单位：千米）（ ）| A． | （0，5） | B． | （5，10） | C． | （10，15） | D． | （15，20） |
分析 建立如图所示的坐标系，t小时后，A（1000t，1000t），B（100，800t），求出|AB|，可得|AB|的最小值，即可得出结论．
解答 解：建立如图所示的坐标系，t小时后，A（1000t，1000t），B（100，800t），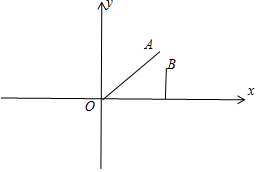
则|AB|=$\sqrt{（1000t-100）^{2}+40000{t}^{2}}$=$\sqrt{1040000{t}^{2}-200000t+10000}$，
t=$\frac{5}{52}$时，|AB|的最小值为$\sqrt{\frac{4×1040000×10000-20000{0}^{2}}{4×1040000}}$=$\frac{50\sqrt{26}}{13}$∈（15，20）．
故选D．
点评 本题考查坐标系的运用，考查距离公式，属于中档题．
练习册系列答案
手拉手全优练考卷系列答案
相关题目
如图，在三棱柱ABC-A1B1C1中，CC1⊥底面ABC，AC⊥CB，点M和N分别是B1C1和BC的中点．
5．函数y=logax（a＞0且a≠1）的图象经过点$（\;2\sqrt{2}\;，\;-1\;）$，函数y=bx（b＞0且b≠1）的图象经过点$（\;1\;，\;2\sqrt{2}）$，则下列关系式中正确的是（ ）
| A． | a2＞b2 | B． | 2a＞2b | C． | ${（{\frac{1}{2}}）^a}＞{（{\frac{1}{2}}）^b}$ | D． | （a${\;}^{\frac{1}{2}}$＞b${\;}^{\frac{1}{2}}$） |
9．数独游戏越来越受人们喜爱，今年某地区科技馆组织数独比赛，该区甲、乙、丙、丁四所学校的学生积极参赛，参赛学生的人数如表所示：
为了解参赛学生的数独水平，该科技馆采用分层抽样的方法从这四所中学的参赛学生中抽取30名参加问卷调查．
（Ⅰ）问甲、乙、丙、丁四所中学各抽取多少名学生？
（Ⅱ）从参加问卷调查的30名学生中随机抽取2名，求这2名学生来自同一所中学的概率；
（Ⅲ）在参加问卷调查的30名学生中，从来自甲、丙两所中学的学生中随机抽取2名，用X表示抽得甲中学的学生人数，求X的分布列．
| 中学 | 甲 | 乙 | 丙 | 丁 |
| 人数 | 30 | 40 | 20 | 10 |
（Ⅰ）问甲、乙、丙、丁四所中学各抽取多少名学生？
（Ⅱ）从参加问卷调查的30名学生中随机抽取2名，求这2名学生来自同一所中学的概率；
（Ⅲ）在参加问卷调查的30名学生中，从来自甲、丙两所中学的学生中随机抽取2名，用X表示抽得甲中学的学生人数，求X的分布列．