题目内容
13．
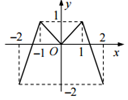如图，定义在[-2，2]的偶函数f（x）的图象如图所示，函数g（x）=f（x）-$\frac{1}{4}x+\frac{1}{2}$的零点个数为（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
分析 问题转化为f（x）和y=$\frac{1}{4}$x-$\frac{1}{2}$的交点个数，画出函数图象，求出交点个数即可．
解答 解：函数g（x）=f（x）-$\frac{1}{4}x+\frac{1}{2}$的零点个数，
即f（x）和y=$\frac{1}{4}$x-$\frac{1}{2}$的交点个数，
画出函数f（x）和y=$\frac{1}{4}$x-$\frac{1}{2}$的图象，如图示：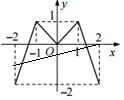
，
显然图象有2个交点，
故函数g（x）=f（x）-$\frac{1}{4}x+\frac{1}{2}$的零点个数为2个，
故选：B．
点评 本题考查了函数图象问题，考查函数零点问题，是一道基础题．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
3．$cos\frac{2017π}{3}$等于（ ）
| A． | $-\frac{1}{2}$ | B． | $\frac{1}{2}$ | C． | $-\frac{{\sqrt{3}}}{2}$ | D． | $\frac{{\sqrt{3}}}{2}$ |
4．设F1，F2分别为双曲线C：$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1（a＞0，b＞0）$的两个焦点，M，N是双曲线C的一条渐近线上的两点，四边形MF1NF2为矩形，A为双曲线的一个顶点，若△AMN的面积为$\frac{1}{2}{c}^{2}$，则该双曲线的离心率为（ ）
| A． | 3 | B． | 2 | C． | $\sqrt{3}$ | D． | $\sqrt{2}$ |
1．如图是函数f（x）=cos（πx+φ）（0＜φ＜$\frac{π}{2}$）的部分图象，则f（3x0）=（ ）
| A． | $\frac{1}{2}$ | B． | -$\frac{1}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | -$\frac{\sqrt{3}}{2}$ |
如图，在平行六面体ABCD-A1B1C1D1中，底面是边长为2的正方形，若$∠{A_1}AB=∠{A_1}AD={60^0}$，且A1A=3，则A1C的长为$\sqrt{17}$．
5．函数y=logax（a＞0且a≠1）的图象经过点$（\;2\sqrt{2}\;，\;-1\;）$，函数y=bx（b＞0且b≠1）的图象经过点$（\;1\;，\;2\sqrt{2}）$，则下列关系式中正确的是（ ）
| A． | a2＞b2 | B． | 2a＞2b | C． | ${（{\frac{1}{2}}）^a}＞{（{\frac{1}{2}}）^b}$ | D． | （a${\;}^{\frac{1}{2}}$＞b${\;}^{\frac{1}{2}}$） |