题目内容
平面向量
，
满足|
|=
|
|，且（
-
）⊥
，则
与
的夹角为（ ）
| a |
| b |
| b |
| 2 |
| a |
| b |
| a |
| a |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
| D、不确定 |
考点：数量积表示两个向量的夹角
专题：平面向量及应用
分析：根据两向量垂直的充要条件：两向量的数量积为0，所以得到：
•
=
2，根据向量的夹角公式以及条件|
|=
|
|即可求出向量
，
的夹角．
| b |
| a |
| a |
| b |
| 2 |
| a |
| a |
| b |
解答：
解：∵(
-
)⊥
，∴(
-
)•
=
•
-
2=0；
∴
•
=
2，设向量
，
夹角为θ，则：
cosθ=
=
=
=
；
∴θ=
．
故选A．
| b |
| a |
| a |
| b |
| a |
| a |
| b |
| a |
| a |
∴
| b |
| a |
| a |
| a |
| b |
cosθ=
| ||||
|
|
| ||||
|
|
|
| ||
|
|
| ||
| 2 |
∴θ=
| π |
| 4 |
故选A．
点评：考查向量垂直的充要条件，向量的数量积，两向量夹角的余弦公式．
练习册系列答案
相关题目
已知函数y=loga（x-1）+3（a＞0，a≠1）所过定点的横、纵坐标分别是等差数列{an}的第二项与第三项，若bn=
，数列{bn}的前n项和为Tn，则T10=（ ）
| 1 |
| an-an+1 |
A、
| ||
B、
| ||
| C、1 | ||
D、
|
下列函数中，在其定义域内为减函数的是（ ）
| A、y=-x3 | ||
B、y=x
| ||
| C、y=x2 | ||
| D、y=log2x |
若点（a，4）在函数y=2x的图象上，则cos
的值为（ ）
| aπ |
| 3 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|
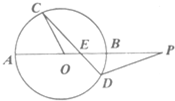如图；圆O的割线PA过圆心O交圆于另一点B，弦CD交OB于点E，且△COE～△POE，PB=OA=2，则PE的长等于（ ）