题目内容
已知向量
，
，
满足：|
|=3，|
|=2，
与
夹角为60°，
=
+
，则
•
的值为（ ）
| OA |
| OB |
| OC |
| OA |
| OB |
| OA |
| OB |
| OC |
| 1 |
| 3 |
| OA |
| 1 |
| 2 |
| OB |
| AC |
| BC |
A、-
| ||
B、
| ||
C、
| ||
| D、2 |
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：先求得向量OA，OB的数量积，再用
=
-
，展开
•
并化简，整理合并，运用向量的平方即模的平方，即可得到结果．
| AB |
| OB |
| OA |
| AC |
| BC |
解答：
解：∵|
|=3，|
|=2，与夹角为60°，
=
+
，
∴
•
=3×2•cos60°=3，
∴
•
=（
-
）•（
-
）=（
-
）•（
-
）
=-
2-
2+
•
=-
×9-
×4+
×3=-
．
故选A．
| OA |
| OB |
| OC |
| 1 |
| 3 |
| OA |
| 1 |
| 2 |
∴
| OA |
| OB |
∴
| AC |
| BC |
| OC |
| OA |
| OC |
| OB |
| 1 |
| 2 |
| OB |
| 2 |
| 3 |
| OA |
| 1 |
| 3 |
| OA |
| 1 |
| 2 |
| OB |
=-
| 2 |
| 9 |
| OA |
| 1 |
| 4 |
| OB |
| 1 |
| 2 |
| OA |
| OB |
| 2 |
| 9 |
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 2 |
故选A．
点评：本题主要考查平面向量的数量积的定义及性质，向量的平方等于模的平方，考查运算能力，属于基础题．
练习册系列答案
相关题目
已知向量
，
，
且满足
+
+
=
，|
|=3，|
|=4，|
|=5，设
与
的夹角为θ1，
与
的夹角为θ2，
与
的夹角为θ3，则它们的大小关系是（ ）
| a |
| b |
| c |
| a |
| b |
| c |
| 0 |
| a |
| b |
| c |
| a |
| b |
| b |
| c |
| a |
| c |
| A、θ1＜θ2＜θ3 |
| B、θ1＜θ3＜θ2 |
| C、θ2＜θ3＜θ1 |
| D、θ3＜θ2＜θ1 |
已知定义在R上的奇函数f（x）满足f（x+2e）=-f（x）（其中e=2.7182…），且在区间[e，2e]上是减函数，令a=
，b=
，c=
，则f（a），f（b），f（c） 的大小关系（用不等号连接）为（ ）
| ln2 |
| 2 |
| ln3 |
| 3 |
| ln5 |
| 5 |
| A、f（b）＞f（a）＞f（c） |
| B、f（b）＞f（c）＞f（a） |
| C、f（a）＞f（b）＞f（c） |
| D、f（a）＞f（c）＞f（b） |
用反证法证明命题“假设三角形内角至多少有一个不大于60°”时，反设正确的是（ ）
| A、假设三角形内角都不大于60° |
| B、假设三角形内角都大于60° |
| C、假设三角形内角至多少有一个大于60° |
| D、假设三角形内角至多少有两个大于60° |
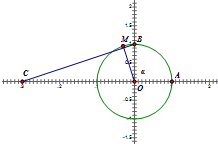如图，A、B是单位圆与x轴、y轴正半轴的交点，点M在单位圆上，∠AOM=α（0＜α＜π），点C（-3，0），若BC⊥OM，则sin（2α-| π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
平面向量
，
满足|
|=
|
|，且（
-
）⊥
，则
与
的夹角为（ ）
| a |
| b |
| b |
| 2 |
| a |
| b |
| a |
| a |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
| D、不确定 |