题目内容
设△ABC的三个内角分别为A,B,C,向量
=(1,sin
+
cos
)与
=(cos
,
)共线.
(Ⅰ)求角C的大小;
(Ⅱ)若D是BC边上一点,AC=2
,AD=2,求钝角△ACD的中线AE的长度.
| m |
| C |
| 2 |
| 3 |
| C |
| 2 |
| n |
| C |
| 2 |
| ||
| 2 |
(Ⅰ)求角C的大小;
(Ⅱ)若D是BC边上一点,AC=2
| 3 |
考点:余弦定理的应用,平面向量的综合题
专题:三角函数的图像与性质
分析:(Ⅰ)通过向量平行,利用两角和与差的三角函数化简求出角C的大小;
(Ⅱ)通过D是BC边上一点,AC=2
,AD=2,利用正弦定理判断∠ADC,通过余弦定理求钝角△ACD的中线AE的长度.
(Ⅱ)通过D是BC边上一点,AC=2
| 3 |
解答:
解:(Ⅰ)∵向量
=(1,sin
+
cos
)与
=(cos
,
)共线,
∴
=cos
(sin
+
cos
)=sin
cos
+
cos2
=
sinC+
cosC+
=sin(C+
)+
∴sin(C+
)=1,
∴C=
.
(Ⅱ)由正弦定理,
=
,
∴∠ADC=60°或120°,
∵△ACD是钝角三角形,∴∠ADC=120°,∴CD=AD=2,∴CE=
CD=1,
由余弦定理:AE2=AC2+CE2-2AC•CEcosC,
∴AE2=12+1-4
•
=7,
∴AE=
.
| m |
| C |
| 2 |
| 3 |
| C |
| 2 |
| n |
| C |
| 2 |
| ||
| 2 |
∴
| ||
| 2 |
| C |
| 2 |
| C |
| 2 |
| 3 |
| C |
| 2 |
| C |
| 2 |
| C |
| 2 |
| 3 |
| C |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| π |
| 3 |
| ||
| 2 |
∴sin(C+
| π |
| 3 |
∴C=
| π |
| 6 |
(Ⅱ)由正弦定理,
2
| ||
| sin∠ADC |
| 2 | ||
sin
|
∴∠ADC=60°或120°,
∵△ACD是钝角三角形,∴∠ADC=120°,∴CD=AD=2,∴CE=
| 1 |
| 2 |
由余弦定理:AE2=AC2+CE2-2AC•CEcosC,
∴AE2=12+1-4
| 3 |
| ||
| 2 |
∴AE=
| 7 |
点评:本题考查余弦定理以及正弦定理的应用,向量的平行,考查计算能力.

练习册系列答案
相关题目
平面向量
,
满足|
|=
|
|,且(
-
)⊥
,则
与
的夹角为( )
| a |
| b |
| b |
| 2 |
| a |
| b |
| a |
| a |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
| D、不确定 |
三个数60.5,0.56,log0.56的大小顺序为( )
| A、log0.56<0.56<60.5 |
| B、log0.56<60.5<0.56 |
| C、0.56<60.5<log0.56 |
| D、0.56<log0.56<60.5 |
若点(m,n)在圆C:x2+y2=4的圆外,则直线l:mx+ny=4与圆C的关系是( )
| A、相离 | B、相切 |
| C、相交 | D、由m、n决定 |
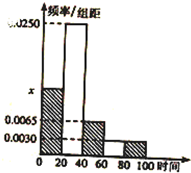 某公司对夏季室外工作人员规定如下:当气温超过35℃时,室外连续工作时间严禁超过100分钟;不少于60分钟的,公司给予适当补助.随机抽取部分工人调查其高温室外连续工作时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中工作时间范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].
某公司对夏季室外工作人员规定如下:当气温超过35℃时,室外连续工作时间严禁超过100分钟;不少于60分钟的,公司给予适当补助.随机抽取部分工人调查其高温室外连续工作时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中工作时间范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].