题目内容
已知函数f(x)=ax2+bx+c和函数g(x)=ax2+bx+clnx(a、b、c∈R,abc≠0).
(Ⅰ)若a=c=-1,且函数g(x)在(0,+∞)递减,求b的取值范围;
(Ⅱ)我们知道“对于函数f(x)=ax2+bx+c,在其图象上任意取不同两点A(x1,y1),B(x2,y2),线段AB中点的横坐标为x0,则直线AB的斜率k=f′(x0)”.
(i)请证明该结论;
(ii)试探究g(x)=ax2+bx+clnx是否也具有该性质.
(Ⅰ)若a=c=-1,且函数g(x)在(0,+∞)递减,求b的取值范围;
(Ⅱ)我们知道“对于函数f(x)=ax2+bx+c,在其图象上任意取不同两点A(x1,y1),B(x2,y2),线段AB中点的横坐标为x0,则直线AB的斜率k=f′(x0)”.
(i)请证明该结论;
(ii)试探究g(x)=ax2+bx+clnx是否也具有该性质.
考点:二次函数的性质
专题:函数的性质及应用
分析:(I)由题意可得g′(x)=
≤0 在(0,+∞)上恒成立,即b≤2x+
.利用基本不等式求得2x+
的最小值,可得b的范围.
(II)(i) 由题意可得 k=
=2x0a+b.由f′(x)=2ax+b 可得f′(x0)=2ax0+b,则k=f′(x0).
(ii)不妨设x2>x1,对于函数g(x)求得 k=2ax0+b+
.如果有该的性质,则 g′(x0)=k,故有
=
.不妨令t=
>1,则
=
(*)成立,即s(t)=lnt-
=0成立.由 s′(t)>0,可得s(t)在(1,+∞)上递增,故有 s(t)>s(1)=0,可得(*)式不成立,由此得出结论.
| 2x2-bx+1 |
| x |
| 1 |
| x |
| 1 |
| x |
(II)(i) 由题意可得 k=
| f(x2)-f(x1) |
| x2-x1 |
(ii)不妨设x2>x1,对于函数g(x)求得 k=2ax0+b+
cln
| ||
| x2-x1 |
ln
| ||
| x2-x1 |
| 2 |
| x2+x1 |
| x2 |
| x1 |
| lnt |
| t-1 |
| 2 |
| t+1 |
| 2t-2 |
| t+1 |
解答:
解:(I)∵a=c=-1,且函数g(x)=-x2+bx-lnx 在(0,+∞)递减,
∴g′(x)=
≤0 在(0,+∞)上恒成立,即b≤2x+
.
又2x+
≥2
,当且仅当x=
时取等号,故b≤2
.
故要求的b的取值范围为(-∞,2
].
(II)(i) 由题意可得 k=
=
=2x0a+b.
由f′(x)=2ax+b 可得f′(x0)=2ax0+b,则k=f′(x0).
(ii)不妨设x2>x1,函数g(x)=ax2+bx+clnx,
∵k=
=
=2ax0+b+
,
又g′(x0)=2ax0+b+
,如果有该的性质,则 g′(x0)=k,
即
=
,c≠0,∴
=
.
不妨令t=
>1,则
=
,(*),即s(t)=lnt-
=0成立.
∵s′(t)=
-
=
>0,
∴s(t)在(1,+∞)上递增,∴s(t)>s(1)=0,即s(t)=0不成立,∴(*)式不成立,即g′(x0)≠k.
∴函数g(x)=ax2+bx+clnx 不具有(II)中的性质.
∴g′(x)=
| 2x2-bx+1 |
| x |
| 1 |
| x |
又2x+
| 1 |
| x |
| 2 |
| ||
| 2 |
| 2 |
故要求的b的取值范围为(-∞,2
| 2 |
(II)(i) 由题意可得 k=
| f(x2)-f(x1) |
| x2-x1 |
| a( x22-x12)+b(x2-x1) |
| x2-x1 |
由f′(x)=2ax+b 可得f′(x0)=2ax0+b,则k=f′(x0).
(ii)不妨设x2>x1,函数g(x)=ax2+bx+clnx,
∵k=
| g(x2)-g(x1) |
| x2-x1 |
a( x22-x12)+b(x2-x1)+c•ln
| ||
| x2-x1 |
cln
| ||
| x2-x1 |
又g′(x0)=2ax0+b+
| c |
| x0 |
即
cln
| ||
| x2-x1 |
| c |
| x0 |
ln
| ||
| x2-x1 |
| 2 |
| x2+x1 |
不妨令t=
| x2 |
| x1 |
| lnt |
| t-1 |
| 2 |
| t+1 |
| 2t-2 |
| t+1 |
∵s′(t)=
| 1 |
| t |
| 2(t+1)-2(t-1) |
| (t+1)2 |
| (t-1)2 |
| t(t+1)2 |
∴s(t)在(1,+∞)上递增,∴s(t)>s(1)=0,即s(t)=0不成立,∴(*)式不成立,即g′(x0)≠k.
∴函数g(x)=ax2+bx+clnx 不具有(II)中的性质.
点评:本题主要考查而粗函数的性质应用,利用导数研究函数的单调性,属于中档题.

练习册系列答案
相关题目
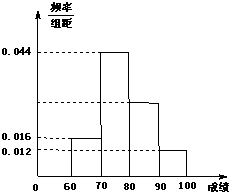 某校50名学生在一次科普知识竞赛中,初赛成绩全部介于60与100之间,将初赛成绩按如下方式分成四组:第一组[60,70],第二组[70,80],…,第四组[90,100].如图是按上述分组方法得到的频率分布直方图.
某校50名学生在一次科普知识竞赛中,初赛成绩全部介于60与100之间,将初赛成绩按如下方式分成四组:第一组[60,70],第二组[70,80],…,第四组[90,100].如图是按上述分组方法得到的频率分布直方图.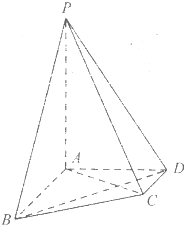 在四棱锥p-ABCD中,AB∥CD,AB⊥AD,AB=4,AD=
在四棱锥p-ABCD中,AB∥CD,AB⊥AD,AB=4,AD=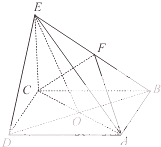 在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.
在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.