题目内容
设a=∫
sinxdx,则二项式(a
-
)6的展开式中含有x2的项的系数为 .
π 0 |
| x |
| 1 | ||
|
考点:二项式定理的应用,定积分
专题:二项式定理
分析:利用定积分求出a,通过二项式定理的通项公式求出通项,通过x的指数为2求出项数,然后求解即可.
解答:
解:由题意a=∫
sinxdx=(-cosx)
=2,
∴二项式为(2
-
)6,设展开式中第r项为Tr+1,
所以Tr+1=
(2
)6-r(-
)r=(-1)r
•26-r•x3-r,令3-r=2,解得r=1.
代入得展开式中x2项的系数为:(-1)
•26-1•=-192.
故答案为:-192.
π 0 |
| | | π 0 |
∴二项式为(2
| x |
| 1 | ||
|
所以Tr+1=
| C | r 6 |
| x |
| 1 | ||
|
| C | r 6 |
代入得展开式中x2项的系数为:(-1)
| C | 1 6 |
故答案为:-192.
点评:本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于中档题.

练习册系列答案
相关题目
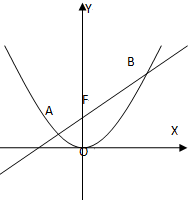 已知直线l经过抛物线x2=4y的焦点,且与抛物线交于A,B两点,点O为坐标原点.
已知直线l经过抛物线x2=4y的焦点,且与抛物线交于A,B两点,点O为坐标原点. 如图是正方体的平面展开图,则在这个正方体中,正确的是
如图是正方体的平面展开图,则在这个正方体中,正确的是