题目内容
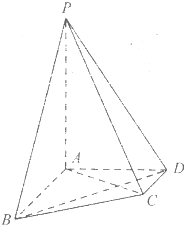 在四棱锥p-ABCD中,AB∥CD,AB⊥AD,AB=4,AD=2
在四棱锥p-ABCD中,AB∥CD,AB⊥AD,AB=4,AD=2| 2 |
(1)求证BD⊥平面PAC;
(2)求二面角A-PC-B的余弦值;
(3)设点Q为线段PB上一点,且直线QC与平面PAC所成角的正弦值为
| ||
| 3 |
| PQ |
| PB |
考点:二面角的平面角及求法,直线与平面垂直的判定,直线与平面所成的角
专题:空间位置关系与距离,空间角
分析:(1)根据线面垂直的判定定理即可证明BD⊥平面PAC;
(2)建立坐标系,利用向量法即可求二面角A-PC-B的余弦值;
(3)利用向量法,即可求出直线和平面所成的角.
(2)建立坐标系,利用向量法即可求二面角A-PC-B的余弦值;
(3)利用向量法,即可求出直线和平面所成的角.
解答:
解:(1)建立空间坐标系如图:
∵AB=4,AD=2
,CD=2,PA=4.
∴A(0,0,0),B(4,0,0),D(0,2
,0),
C(2,2
,0),P(0,0,4),
∵PA⊥平面ABCD,
∴PA⊥BD,
∵
=(2,2
,0),
=(-4,2
,0),
∴
•
=-8+8=0,
即
⊥
,则BD⊥AC,
∵AC∩PA=A,
∴BD⊥平面PAC
(2)∵BD⊥平面PAC
∴
=(-4,2
,0)是平面PAC的法向量,
设平面PCB的法向量为
=(x,y,z),
则
=(-4,0,4),
=(-2,-2
,4),
则
,
令z=1,则x=1,y=
,即
=(1,
.1),
则二面角A-PC-B的余弦值|cos<
,
>|=|
|=
=
.
(3)
=(-4,2
,0)是平面PAC的法向量,
若直线QC与平面PAC所成角的正弦值为
,
即
与
所成角的余弦值的绝对值为
,
设
=m,则
=m
=m(4,0,-4)=(4m,0,-4m),
则
=
+
=(-2,-2
,4)+(4m,0,-4m)=(4m-2,-2
,4-4m),
则|cos<
,
>|=|
|=|
|=
,
即|
|=
,
解得m=
,
即
=
.
∵AB=4,AD=2
| 2 |
∴A(0,0,0),B(4,0,0),D(0,2
| 2 |
C(2,2
| 2 |
∵PA⊥平面ABCD,
∴PA⊥BD,
∵
| AC |
| 2 |
| BD |
| 2 |

∴
| AC |
| BD |
即
| AC |
| BD |
∵AC∩PA=A,
∴BD⊥平面PAC
(2)∵BD⊥平面PAC
∴
| BD |
| 2 |
设平面PCB的法向量为
| n |
则
| BP |
| CP |
| 2 |
则
|
令z=1,则x=1,y=
| ||
| 2 |
| n |
| ||
| 2 |
则二面角A-PC-B的余弦值|cos<
| BD |
| n |
-4+2
| ||||||
|
| 2 | ||
2
|
| ||
| 15 |
(3)
| BD |
| 2 |
若直线QC与平面PAC所成角的正弦值为
| ||
| 3 |
即
| CQ |
| BD |
| ||
| 3 |
设
| PQ |
| PB |
| PQ |
| PB |
则
| CQ |
| CP |
| PQ |
| 2 |
| 2 |
则|cos<
| CQ |
| BD |
| ||||
|
|
| -4(4m-2)+8+4(4-4m) | ||||
|
| ||
| 3 |
即|
| -32m+32 | ||||
|
| ||
| 3 |
解得m=
| 7 |
| 12 |
即
| PQ |
| PB |
| 7 |
| 12 |
点评:本题主要考查空间直线和平面垂直的判断,以及空间二面角和直线和平面所成角计算,利用向量法是解决本题的关键.

练习册系列答案
相关题目
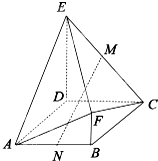 多面体ABCDEF中,M、N分别为EC、AB的中点,底面ABCD为菱形,且∠BAD=
多面体ABCDEF中,M、N分别为EC、AB的中点,底面ABCD为菱形,且∠BAD=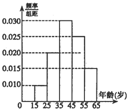 某市交管部门为了宣传新交规举办交通知识问答活动,随机对该市15~65岁的人群抽样了n人,回答问题统计结果如图表所示:
某市交管部门为了宣传新交规举办交通知识问答活动,随机对该市15~65岁的人群抽样了n人,回答问题统计结果如图表所示: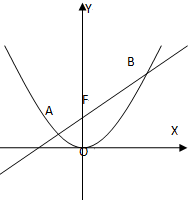 已知直线l经过抛物线x2=4y的焦点,且与抛物线交于A,B两点,点O为坐标原点.
已知直线l经过抛物线x2=4y的焦点,且与抛物线交于A,B两点,点O为坐标原点.